4.5. АЛГОРИТМ ТИПУ "РОЗПОДІЛЯЙ ТА ВОЛОДАРЮЙ"
Припустимо, що при розв'язанні задачі побудови опуклої оболонки, початкова множина точок була розбита на дві частини (S1 і S2 ), кожна з яких містить половину точок початкової множини.
Якщо тепер рекурсивним чином знайдені окремо CH(S1)
і CH(S2), то які додаткові витрати, необхідні для побудови CH(S1 S2), тобто ОО початкової множини? Для відповіді на це питання можна скористатись таким співвідношенням:
S2), тобто ОО початкової множини? Для відповіді на це питання можна скористатись таким співвідношенням:
CH(S1  S2)= CH(CH(S1)
S2)= CH(CH(S1)  CH(S2))
CH(S2)) (4.2)
Головна думка полягає в тому, що CH(S1) і CH(S2)- це не просто невпорядковані множини точок, а опуклі многокутники (мал. 4.9).
Мал. 4.9. Побудова опуклої оболонки методом "розподіляй та володарюй".
Задача ОО3. (ОПУКЛА ОБОЛОНКА ОБ'ЄДНАННЯ ОПУКЛИХ МНОГОКУТНИКІВ). Задано два опуклих многокутники Р1 і Р2. Знайти опуклу оболонку їх об'єднання. Загальна схема розв'язання цієї задачі матиме такий вигляд:
procedura СЛИБОЛ(S)
- |S|
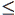 k0 (k0- деяке невелике ціле число), то побудувати опуклу оболонку одним із прямих методів і зупинитись; інакше перейти до кроку 2.
k0 (k0- деяке невелике ціле число), то побудувати опуклу оболонку одним із прямих методів і зупинитись; інакше перейти до кроку 2.
- Розбити початкову множину S довільним чином на дві приблизно рівні за потужністю підмножини S1 і S2.
- Рекурсивно знайти опуклі оболонки S1 і S2.
- Злити (об'єднати) дві отримані оболонки разом, утворюючи CH(S).
Позначимо символом U(N) час, необхідний для знаходження ОО об'єднання опуклих многокутників, кожен з яких має N/2 вершин. Якщо Т(N)- час, необхідний для знаходження ОО множини із N точок, то, використовуючи співвідношення (4.2), отримаємо:
Т(N) 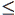 2T(N/2) + U(N).
2T(N/2) + U(N). (4.3)
Алгоритм "злиття", запропонований М. Шеймосом.
procedura ОБОЛОНКА_ОБ'ЄДНАННЯ_ОПУКЛИХ_МНОГОКУТНИКІВ(Р1, Р2).
- Знайти деяку внутрішню точку р многокутника Р1. (Наприклад, центроїд трьох довільних вершин Р1. Така точка р буде внутрішньою точкою CH(P1
 P2)).
P2)).
- Визначити, чи є р внутрішньою точкою Р2. Це може бути зроблено за час
О(N). Якщо р не є внутрішньою точкою Р2, перейти до кроку 4.
- р є внутрішньою точкою Р2 (мал. 4.10). За теоремою 4.5 вершини як Р1, так і Р2 виявляються впорядкованими відповідно до значення полярного кута відносно точки р. За час О(N) можна отримати впорядкований список вершин як Р1, так і Р2 шляхом злиття списків вершин цих многокутників.
Перейти до кроку 5.
Мал. 4.10. Точка р знаходиться всередині многокутника Р2.
- р не є внутрішньою точкою Р2 (мал. 4.11). Якщо дивитись із точки р, то многокутник Р2 лежить у клині з кутом розвороту, який є меншим або рівним p. Цей клин визначається двома вершинами u і v многокутника Р2, які можуть бути знайдені за лінійний час за один обхід вершин многокутника Р2. Ці вершини розбивають границю Р2 на два ланцюги вершин, які є монотонними відносно зміни полярного кута з початком в р. Один із цих двох ланцюгів, яки є опуклим за напрямком до точки р, може бути відразу вилученим, так як його вершини будуть внутрішніми точками CH(S1
 S2). Інший ланцюг Р2 і границя Р1 являють собою два впорядкованих списки, які містять у сумі не більше N вершин. За час О(N) їх можна злити в один список вершин P1
S2). Інший ланцюг Р2 і границя Р1 являють собою два впорядкованих списки, які містять у сумі не більше N вершин. За час О(N) їх можна злити в один список вершин P1 Р2, упорядкованих за кутом відносно точки р.
Р2, упорядкованих за кутом відносно точки р.
- До отриманого списку можна застосувати метод обходу Грехема, який вимагає лише лінійного часу. Результат - опукла оболонка P1
 P2.
P2.
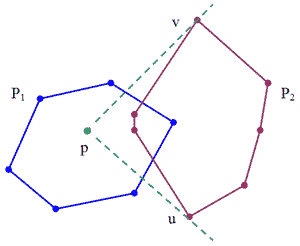
Мал 4.11. Точка р знаходиться зовні многокутника Р2.
Якщо многокутник Р1 має m вершин,
а Р2 має n вершин,
то час виконання цього алгоритму дорівнює О(m+n), що є оптимальним.
Таким чином час злиття лінійний і U(N)=O(N), а розв'язок рекурентного співвідношення (4.3) в цьому випадку є Т(N) = О(Nlog N). Як висновок має місце теорема:
Теорема 4.8 Опукла оболонка об'єднання двох опуклих многокутників може бути знайдена за час, пропорційний сумарному числу їх вершин.
Означення 4.5 Опорною прямою до опуклого многокутника Р називається пряма l, яка проходить через деяку вершину многокутника Р таким чином, що внутрішня частина Р повністю знаходиться по одну сторону від l (в деякому розумінні поняття опорної прямої аналогічне поняттю дотичної).
Очевидно, що два опуклих многокутники Р1 і Р2 з n і m вершинами відповідно, таких, що один не лежить всередині іншого, мають загальні опорні прямі ( принаймні не більше 2min(n,m)). Якщо вже побудована ОО об'єднання Р1 і Р2, то опорні прямі обчислюються в результаті перегляду списку вершин СН(Р1 Р2). Кожна пара послідовних вершин СН(Р1
Р2). Кожна пара послідовних вершин СН(Р1 Р2), одна з яких належить Р1, а інша Р2, визначає опорну пряму.
Р2), одна з яких належить Р1, а інша Р2, визначає опорну пряму.
 S2)
S2) S2), тобто ОО початкової множини? Для відповіді на це питання можна скористатись таким співвідношенням:
S2), тобто ОО початкової множини? Для відповіді на це питання можна скористатись таким співвідношенням:
 S2)= CH(CH(S1)
S2)= CH(CH(S1)  CH(S2)) (4.2)
CH(S2)) (4.2)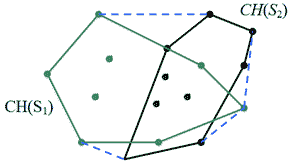
 k0 (k0- деяке невелике ціле число), то побудувати опуклу оболонку одним із прямих методів і зупинитись; інакше перейти до кроку 2.
k0 (k0- деяке невелике ціле число), то побудувати опуклу оболонку одним із прямих методів і зупинитись; інакше перейти до кроку 2. 2T(N/2) + U(N). (4.3)
2T(N/2) + U(N). (4.3) P2)).
P2)).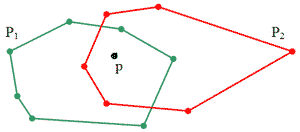
 S2). Інший ланцюг Р2 і границя Р1 являють собою два впорядкованих списки, які містять у сумі не більше N вершин. За час О(N) їх можна злити в один список вершин P1
S2). Інший ланцюг Р2 і границя Р1 являють собою два впорядкованих списки, які містять у сумі не більше N вершин. За час О(N) їх можна злити в один список вершин P1 Р2, упорядкованих за кутом відносно точки р.
Р2, упорядкованих за кутом відносно точки р. P2.
P2.
 Р2). Кожна пара послідовних вершин СН(Р1
Р2). Кожна пара послідовних вершин СН(Р1 Р2), одна з яких належить Р1, а інша Р2, визначає опорну пряму.
Р2), одна з яких належить Р1, а інша Р2, визначає опорну пряму.