4.4.ШВИДКІ МЕТОДИ ПОБУДОВИ ОПУКЛОЇ ОБОЛОНКИ.
Задача сортування є джерелом натхнення в розробці ідей побудови ОО. Зокрема, майже одночасно в роботах деяких авторів (Eddy(1977); Bykat (1978); Green, Silverman (1979); Floyd (1976)) подається ідея алгоритмів швидкого сортування. Через їх близькість з алгоритмом ШВИДКОСОРТ дамо їм назву - швидкі методи побудови опуклої оболонки або ШВИДКОБОЛ.
Коротко нагадаємо ідею алгоритму ШВИДКОСОРТ [2].
Є масив із N чисел, необхідно розбити його на лівий і
правий підмасиви так, щоб кожен елемент першого підмасиву не перевищував кожний із елементів другого підмасиву.
Це робиться за допомогою двох вказівників на елементи масиву, встановлених на початку відповідно на два крайніх елементи масиву, які переміщуються назутріч один одному на один елемент за один крок обробки. Кожного разу, якщо елементи, на які вказують вказівники, не задовольняють необхідний порядок, здійснюється перестановка цих елементів.
Вказівники рухаються почергово - один рухається, а інший залишається на місті.
Після кожної виконаної перестановки вказівники міняються ролями.
При досягненні вказівниками одного і того ж елементу, масив виявляється розбитим на два підмасиви, і потім до кожного із них окремо застосовується та ж сама процедура.
Такий підхід є ефективним і має оцінку O(N log N), якщо кожний масив розбивається на приблизно рівні частини.
Відповідний ШВИДКОБОЛ-метод розбиває множину S із N точок на дві підмножини, кожна з яких буде містити одну із двох ламаних, з'єднання яких дає многокутник опуклої оболонки.
Алгоритм.
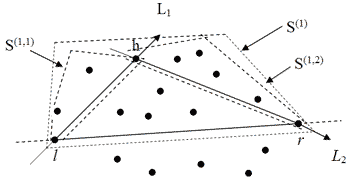
- Початкове розбиття множини визначається прямою, яка проходить через дві точки l і r, які мають відповідно найменшу і найбільшу абсциси ( мал. 4.8). Позначимо через S(1) підмножину точок, які розташовані вище або на прямій, яка проходить через l і r, а через S(2) - симетричним чином визначену підмножину точок, розташованих нижче або на тій же прямій.
Мал. 4.8. Точки l, r і h визначають розбиття множини S(1).
- Визначимо точку h, для якої трикутник ( hlr ) має максимальну площу серед усіх трикутників {(plr): p
S(1)} , а якщо таких точок більше однієї, то вибираємо ту з них, у якої кут 
( hlr ) більший. Зазначимо, що точка h гарантовано належить опуклій оболонці.
- Потім будуються дві прямі: одна L1, спрямована із l в h, інша L2 - із h в r.
Для кожної точки множини S(1) визначається її положення відносно цих прямих. Жодна з точок не знаходиться одночасно ліворуч як від L1, так і від L2, окрім того, усі точки, розташовані праворуч від обох прямих, є внутрішніми точками трикутника (lrh) і тому можуть бути вилучені із подальшої обробки.
Точки, розташовані ліворуч від L1 або на ній ( і розташовані праворуч від L2), утворюють множину S(1,1); аналогічно утворюється множина S(1,2). Утворені множини S(1,1) і S(1,2) передаються на наступний рівень рекурсивної обробки.
Виберемо відповідний набір початкових значень {l0, r0} точок l і r: за l0 візьмемо точку (x0, y0), яка має найменшу абсцису, а за r0 візьмемо точку (x0, y0-e), де e - довільне мале додатне число.
Звідси випливає, що за початкову пряму, яка розбиває множину на частини, обирається вертикальна пряма, яка проходить через точку l0.
Після завершення алгоритму точка r0 вилучається.
Припустимо, що множина S містить принаймні дві точки, а функція САМАДАЛЬНЯТОЧКА (S;l,r) обчислює точку h S описаним вище способом; окрім того, ШВИДКОБОЛ повертає у якості результату впорядкований список точок, а "*" позначає операцію зчеплення(конкатенацію) списків.
function ШВИДКОБОЛ(S;l,r)
- begin if (S={l,r}) then return ( l, r ) (* ОО складається із єдиного орієнтованого ребра *)
- else begin h:= САМАДАЛЬНЯТОЧКА(S;l,r);
- S(1):= точки множини S , розташовані ліворуч від [l,h] або на ній;
- S(2):= точки множини S , розташовані ліворуч від [h,r] або на ній;
return ШВИДКОБОЛ(S(1);l,r) *
(ШВИДКОБОЛ(S(2);h,r)-h)
end
end.
Таким чином, якщо вже маємо функцію ШВИДКОБОЛ, то поставлену задачу можна розв'язати за допомогою такої простої програми:
begin l0=(x0, y0):= точка множини S з найменшою абсцисою;
r0 = (x0, y0 - e);
ШВИДКОБОЛ(S; l0, r0);
вилучити точку r0 (* це еквівалентно тому, що покласти e = 0*)
end
Потім йде рекурсивне звернення до функції для обробки S(1) і S(2). Якщо потужність кожної із цих множин не перевищує потужності множини S, помноженої на деяку константу, меншу за 1, і ця умова має місце на кожному рівні рекурсії, то час виконання алгоритму рівний О(NlogN). Однак, в гіршому випадку ШВИДКОБОЛ, не зважаючи на його простоту, має той же недолік, що і ШВИДКОСОРТ, який дає час виконання О(N2).
