Попередня Змiст Наступна

4.6.ДИНАМІЧНІ АЛГОРИТМИ ПОБУДОВИ ОПУКЛОЇ ОБОЛОНКИ.

У кожному із алгоритмів, що розглядалися раніше, вимагалось, щоб усі дані, які обробляються (а саме точки), були повністю представлені до початку роботи алгоритму. В багатьох прикладних областях, де виникають геометричні задачі, зокрема, пов'язані з обробкою даних в реальному, таке обмеження відсутнє, а ряд обчислень повинен виконуватись в міру надходження точок.
Означення 4.6 Алгоритм, що обробляє дані в міру їх надходження, називається відкритим, а алгоритм, який обробляє всю сукупність у цілому, називається закритим.
Означення 4.7 Будемо називати часовий інтервал між вводом двох послідовних елементів даних затримкою надходження даних.
Означення 4.8 Вважатимемо, що надходження даних відбувається (розподілено) рівномірно за часом. У цьому випадку корекція повинна виконуватися за час, який не перевищує постійної затримки надходження даних. Алгоритми, що працюють у такому режимі, називаються відповідно алгоритмами реального часу.
Задача ОО4 (ВІДКРИТИЙ АЛГОРИТМ ДЛЯ ОПУКЛОЇ ОБОЛОНКИ)
На площині задана послідовність із N точок р1,…,рN. Необхідно знайти їх опуклу оболонку, організувавши обробку таким чином, щоб після обробки точки рi мали СН({p1, …,pi}).
Задача ОО5 (ОПУКЛА ОБОЛОНКА В РЕАЛЬНОМУ ЧАСІ )
На площині задана послідовність із N точок р1,…,рN. Необхідно знайти їх опуклу оболонку за умови, що час затримки надходження точок постійний.
Якщо не брати до уваги час обробки, можна розробити відкритий алгоритм побудови ОО, застосувавши підхід, оснований на алгоритмі Грехема, що складається з двох кроків ( сортування й обходу), а саме:
  1. Вводити точки до тих пір, доки не будуть знайдені три неколінеарні точки. Їх центроїд буде внутрішньою точкою кінцевої ОО і, таким чином, підходить для початку координат, відносно якого визначаються полярні кути точок при сортуванні в алгоритмі ОБОЛОНКА ГРЕХЕМА.
  2. Підтримувати зв'язаний список упорядкованих крайніх точок. При надходженні точки рi тимчасово вставити її в цей список відповідно до її полярного кута, витративши на це час О(і).
  3. Виконати перегляд зв'язаного списку крайніх точок методом Грехема. Так як перегляд методом Грехема лінійний, то необхідно лише О(і) часу. Можливі три варіанти завершення цього кроку:
    1. точка рі є крайньою обробленої на поточний момент множини, і її включення до числа крайніх точок спричиняє вилучення декількох інших точок;
    2. точка рі є крайньою, але ніякі інші точки не вилучаються;
    3. точка рі є внутрішньою для опуклої оболонки, що створюється, і тому вона вилучається.
Загальний час виконання цього алгоритму в гіршому випадку дорівнює О(N2), що має місце, якщо кожна точка є крайньою.
Шеймос розробив алгоритм [1], який для множини із N точок виконується глобально за час О(N log N) і є оптимальним. Суть ідеї полягає у тому, що на кроці 2 попереднього алгоритму замість лінійної вставки робиться бінарна і відповідно до цього на кроці 3 більш ефективно (логарифмічно) виконувати пошук замість використання лінійного перегляду методом Грехема. Але при цьому на корегування витрачається час О( log2 N). Щоб визначити на скільки цей алгоритм відповідає вимогам, які висуваються до алгоритмів для обробки в реальному часі, зазначимо, що нижні оцінки, одержані для закритих алгоритмів, в рівній мірі застосовуються і до відкритих алгоритмів. Цим фактом можна скористатися для одержання нижніх оцінок часу, який відкритий алгоритм повинен витратити на обробку чергової порції даних.
Теорема 4.9 Будь-який відкритий алгоритм побудови опуклої оболонки в гіршому випадку витрачає на обробку між надходженнями послідовних елементів даних час W(logN).
Таким чином, вище згаданий алгоритм не задовольняє вимогам, які висуваються до алгоритмів реального часу. Однак Препарата [1] розробив відкритий алгоритм з тією ж самою глобальною оцінкою часової складності, але з часом корекції О(logN), що збіглося з оцінкою часу затримки надходження, встановленою теоремою 4.9. Розглянемо цей алгоритм.
Алгоритм Препарата.
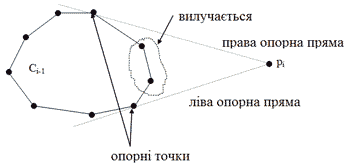
Ключ щодо створення ефективного відкритого алгоритму дають такі міркування: єдине, що необхідно, - це вміти швидко будувати дві опорні прямі до опуклого многокутника, які проходять через деяку точку.
Якщо точки обробляються в порядку р1, р2,... і рі - поточна точка, то позначимо через Сі-1 опуклу оболонку множини { р1, р2, ..., рі-1}. Необхідно побудувати з точки рі опорні прямі до Сі-1 (якщо вони існують). У першому випадку повинна вилучитись відповідна низка вершин, яка міститься між двома опорними точками, а замість них вставляється точка рі (мал. 4.12). Для зручності опорну пряму будемо називати лівою або правою відповідно до того, по яку сторону вона знаходиться, якщо дивитися з точки рі на Сі-1.
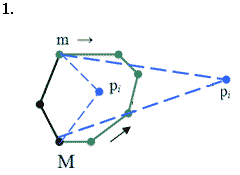
Мал. 4.12. Опорні прямі з точки рі до опуклого многокутника Сі-1.
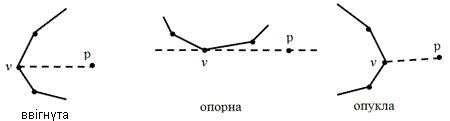
Надалі важливу роль гратиме класифікація вершин многокутника С відносно відрізка [p,v], який з'єднує вершину v з точкою р.
Класифікація вершин. Вершина v називається ввігнутою, якщо відрізок [p,v] перетинає внутрішню частину многокутника С. Інакше, якщо дві суміжні з v вершини лежать по одну сторону від прямої, яка проходить через точки p і v, вершина v називається опорною. У випадку, що залишився, вершина v називається опуклою.
Мал. 4.13. Класифікація вершин v многокутника С відносно відрізка [p,v].
Якщо v - опорна вершина, то на цьому розв'язання задачі завершується. Припустимо, що шукається ліва опорна пряма. Якщо точка v не є опорною, то необхідно рухатися по вершинам многокутника С проти або за годинниковою стрілкою залежно від того, чи є v ввігнутою або опуклою вершиною ( мал. 4.13). Таким способом можна визначити дві опорні точки (якщо вони існують). Якщо це зроблено, необхідно мати можливість вилучити із циклічної послідовності вершин многокутника С низку вершин (можливо, порожню) і вставити в утворений розрив точку р. Виконуються такі операції:
  1. ПОШУК в упорядкованій послідовності елементів (кільцевого списку вершин оболонки) для визначення опорних прямих з точки рі;
  2. РОЗЧЕПЛЕННЯ послідовності на дві послідовності і ЗЧЕПЛЕННЯ двох послідовностей;
  3. ВСТАВКА одного елемента ( поточної точки рі).
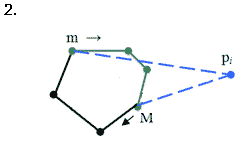
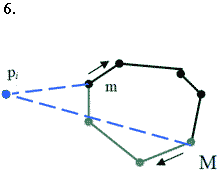
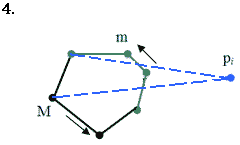
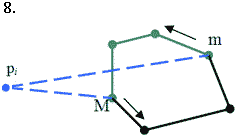
Структура даних, яка в повній мірі задовольняє перераховані вимоги, називається зчепленою чергою. Вона реалізується за допомогою збалансованого за висотою дерева пошуку, і при цьому кожна із вказаних вище операцій виконується за час О(log i) в гіршому випадку, де і - число вузлів дерева. Природно, кільцева послідовність вершин зображається в цій деревовидній структурі даних ланцюгом, і при цьому перший і останній елементи вважаються суміжними. В структурі Т виділяються дві вершини : m- самий лівий член ланцюга і М- кореневий член ланцюга. Крім того, використовується кут (mpiM), який позначимо a. Цей кут називається опуклим, якщо він менший або дорівнює p, і ввігнутим в протилежному випадку.
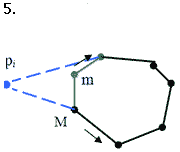
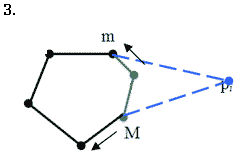
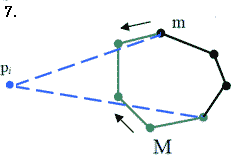
Залежно від класифікації вершин m і М (ввігнута, опорна, опукла) і кута a можливі всього вісімнадцять випадків. Однак всі ці випадки можна звести до восьми( які покривають усі можливі), які наведено у таблиці 1 і показано на малюнку 4.14.
Мал. 4.14. Вісім можливих випадків залежно від класифікації вершин m, М і кута a.
Таблиця 1.
a m M
1 Опуклий Ввігнута Ввігнута
2 Опуклий Ввігнута Неввігнута
3 Опуклий Неввігнута Опукла
4 Опуклаий Неввігнута Неопукла
5 Ввігнутий Опукла Опукла
6 Ввігнутий Опукла Неопукла
7 Ввігнутий Неопукла Ввігнута
8 Ввігнутий Неопукла Неввігнута
Наступна процедура здійснює пошук вершини l:

    function ЛІВИЙ_ПОШУК(Т)
    Input:дерево Т, яке описує послідовність вершин
    Output: вершина l
  1. begin с:=КОРІНЬ(Т);
  2. if (pc-опорна пряма) then l:=c
  3. else begin if (с- опукла вершина) then

    4. Т:=ЛДЕРЕВО(с) else Т:=ПДЕРЕВО(с)
  4. l:=ЛІВИЙ_ПОШУК(Т)

    5. end;
  5. return l

    6. end.
Враховуючи, що дерево Т збалансоване і містить не більше i < N вершин, а на обробку у кожному вузлі вимагається обмежений час, оцінка пошуку буде рівною О(log i).
Як зазначалося раніше, обидві операції РОЗЧЕПИТИ і ЗЧЕПИТИ виконуються за час О(log i). В результаті, враховуючи, що корекція опуклої оболонки може бути виконана за час О(log i), маємо теорему.
Теорема 4.10 Опукла оболонка множини із N точок на площині може бути знайдена за допомогою відкритого алгоритму за час q(NlogN) з часом корекції q(logN), тобто може бути побудована в реальному часі.

Попередня Змiст Наступна