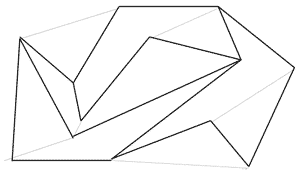
3.3.2. Метод ланцюгів
Означення 3.5 Ланцюгом С = (u1,..., up) називається плоский прямолінійний граф з вершинами {u1,..., up} і ребрами {(ui,ui+1): i = 1,..., p-1}.
Мал. 3.11(а). Ланцюг загального виду.
Розглянемо планарне підрозбиття, яке визначається ППЛГ G. Припустимо, що в G знайдений ланцюг C (підграф G) одного із типів:
- C є циклом.
- обидва кінці u1 і up із C лежать на границі нескінченної області.
В останньому випадку продовжимо C з обох кінців напівнескінченними паралельними протилежно напрямленими ребрами. Ланцюг кожного типу ділить початкове підрозбиття на дві частини.
Означення 3.6 Дискримінацією точки z відносно ланцюга C називається процедура визначення того, по яку сторону від C лежить пробна точка z.
Означення 3.7 Ланцюг С = (u1,..., up) називається монотонним відносно прямої l, якщо будь-яка пряма, ортогональна до l, перетинає С тільки в одній точці.
Означення 3.8 Простий многокутник називається монотонним, якщо його границю можна розбити на два ланцюги, монотонних відносно однієї прямої.
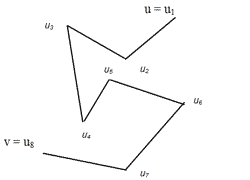
Один із подібних ланцюгів зображено на малюнку 3.11(b):
Мал. 3.11(b).
L(u) = [l(u1), l(u2), l(u3), l(u4), l(u5)], l(p) - проекція на l точки р і ланцюга.
- O(logN)- локалізація l(p) на L(u).
- О(1)- по яку сторону відносно ланцюга розташована точка р.
Означення 3.9. Припустимо, що існує деяка множина Z= {C1,…,Cr} ланцюгів, монотонних відносно однієї і тієї ж прямої l і які мають такі властивості:
Властивість 1. Об'єднання всіх елементів Z містить заданий ППЛГ G.
Властивість 2. Для будь-якої пари ланцюгів Ci і Cj із Z ті вузли Ci, які не є вузлами Cj, лежать по одну сторону від Cj.
Тоді множина Z наз. повною множиною монотонних ланцюгів графа G.
Якщо є r ланцюгів в Z і у найдовшому ланцюзі p вершин, то пошук займе у найгіршому випадку O(logr * logp) часу.
Залишилось найголовніше питання: чи можна побудувати повну множину монотонних ланцюгів для будь-якого плоского прямолінійного графа G? Виявляється не можна. Але можна показати, що плоский прямолінійний граф допускає побудову повної множини монотонних ланцюгів, якщо задовольняє деяке обмеження. Крім того, будь-який плоский прямолінійний граф можна легко перетворити в такий граф, до якого можна застосувати процедуру побудови ланцюгів. Наступне означення являє собою деяке обмеження, яке згадане вище.
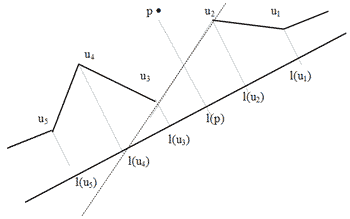
Означення 3.10 Нехай G - плоский прямолінійний граф з множиною вершин {v1,..., vN}, де вершини індексовані так, що i < j тоді і тільки тоді, коли y(vi) < y(vj), або y(vi) = y(vj) і x(vi) < x(vj). Вершина vj називається регулярною, якщо існують такі цілі i < j < k, що (vi, vj) i (vj, vk) - ребра G. Говорять, що плоский прямолінійний граф G регулярний, якщо кожна вершина регулярна при 1 < j < N (за винятком двох крайніх вершин v1 та vN).
Мал. 3.12. Приклад регулярного плоского прямолінійного графу.
Позначимо через IN(vj) та OUT(vj) множини ребер, які входять та виходять з вершини vj. Нехай ребра в IN(vj) впорядковані за кутом проти годинникової стрілки, а ребра в OUT(vj) - за годинниковою стрілкою.
Теорема 3.5. Для довільної vj можна побудувати y - монотонний ланцюг від v1 до vj.
Доведення. Методом математичної індукції:
- для j = 2;
- k < j;
- vj регулярна, то $ i < j, що (vi, vj)
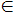 G;
G;
- $ ланцюг C від v1 до vi, монотонний відносно осі y і його з'єднання з ребром (vi, vj) дасть також монотонний ланцюг.
Теорема 3.6 Довільний регулярний граф можна розбити на повну множину ланцюгів, монотонних відносно осі y.
Доведення. Позначимо через W(e) вагу ребра e - кількість ланцюгів, яким належить e. Введемо позначення:
Ваги ребер обираються так, щоб виконувалися умови:
- кожне ребро має додатну вагу;
- для довільного vj (j
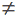 1, N) WIN (vj) = WOUT (vj).
1, N) WIN (vj) = WOUT (vj).
Теорема 3.7 Реалізація умови WIN = WOUT є розв'язком потокової задачі і може бути досягнута за два проходи по графу G.
Покладемо спочатку W(e) = 1 для кожного ребра e. При першому проході від v1 до vN отримаємо WIN (vi) 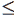 WOUT (vi) для всіх некрайніх vi. При другому проході від vN до v1 отримаємо WIN (vi)
WOUT (vi) для всіх некрайніх vi. При другому проході від vN до v1 отримаємо WIN (vi) 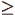 WOUT (vi). Отже після двох проходів матимемо реалізацію умови WIN (vi) = WOUT (vi). Позначимо vIN (v) = | IN(v)|, vOUT (v) = | OUT(v)|.
WOUT (vi). Отже після двох проходів матимемо реалізацію умови WIN (vi) = WOUT (vi). Позначимо vIN (v) = | IN(v)|, vOUT (v) = | OUT(v)|.
Алгоритм балансування за вагою
procedure БАЛАНСУВАННЯ ЗА ВАГОЮ В РЕГУЛЯРНОМУ ППЛГ
begin for кожного ребра е do W(e) := 1 (* ініціалізація *)
for i := 2 to N - 1 do
begin WIN(vi):= сума ваг ребер, які входять в vi;
d1 := крайнє зліва ребро, яке виходить із vi;
if (WIN(vi) > vOUT(vi)) then W(d1):= WIN(vi) - vOUT(vi) + 1
end (* перший прохід *);
for i := N - 1 downto 2 do
begin WOUT(vi):= сума ваг ребер, які виходять із vi;
d2:= крайнє зліва ребро, яке входить в vi;if (WOUT(vi) > WIN(vi)) then W(d2):= WOUT(vi)-WIN(vi)+W(d2)
end (* другий прохід *)
end.
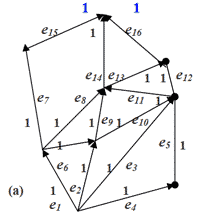
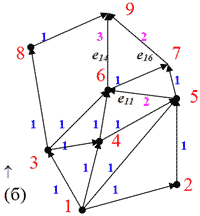
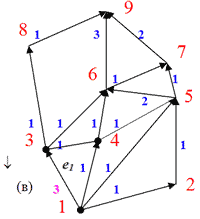
Приклад2. На мал. 3.13(а)-(д) показано конфігурацію ваг ребер після ініціалізації, 1-го та 2-го проходів відповідно і малюнок ланцюгів ППЛГ з мал.3.12.
Для кожного ребра W(e):= 1 (* ініціалізація *)
(5): (WIN(5) = 3 > vOUT(5) = 2) ==> W(e11):= 3-2 + 1=2;
(6): (WIN(6) = 4 > vOUT(6) = 2) ==>W(e14):= 4-2 + 1=3;
(7): (WIN(7) = 2 > vOUT(7) = 1) ==>W(e16):= 2-1 + 1=2;
(3): (WOUT(3) = 3 > WIN(3) = 1) ==>W(e11):= 3-1 + 1=3;
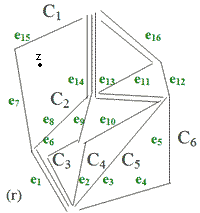
C1 = (e1, e7, e15), C2 = (e1, e8, e14), C3 = (e1, e6, e9, e14),
C4 = (e2, e10, e11 ,e14), C5 = (e3, e11, e13, e16), C6 = (e4, e5, e12, e16).
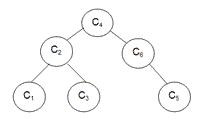
Z = ( C1, C2, C3, C4, C5, C6) - повна множина монотонних ланцюгів.
3.13. Мітки ребер є їхніми вагами після: (а) ініціалізації; (б) першого проходу; (в) другого проходу; (г) повна множина монотонних ланцюгів та відповідне бінарне дерево.
Регуляризація графа
На малюнку 3.14 (a) зображено нерегулярну вершину першого роду (яка не має вхідних ребер), а на малюнку 3.14 (б) - нерегулярну вершину другого роду (яка не має вихідних ребер).
Мал. 3.14(а, б). Приклад типової нерегулярної вершини v.
Теорема 3.8. Довільний планарний граф можна перетворити в регулярний.
Використовуючи алгоритм плоского замітання, замітаємо граф згори донизу, регуляризуючи вершини, які не мають вихідних ребер, а потім знизу вгору для регуляризації вершин, які не мають вхідних ребер.
У процесі замітання для кожної вершини v реалізуємо наступні операції:
- локалізуємо v (по абсцисі) в одному із інтервалів у структурі даних статусу;
- коригуємо цю структуру статусу;
- якщо v нерегулярна, тоді додаємо ребро від v до тієї вершини, яка зв'язана з інтервалом, який визначений в операції (1).
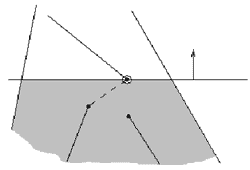
Розглянемо пункт (3) ширше. Очевидно, що для проведення ребер, що будуть регуляризовувати вершини необхідно знати дві вершини. Одна з яких - поточна нерегулярна, інша - та, що зустрічалася на шляху замітаючої прямої на попередньому кроці. Основна проблема при введенні нового ребра полягає у проведені його так, щоб воно не перетинало вже існуючі ребра. Ця умова дозволяє запропонувати такий вибір другої вершини ребра: вибирати таку вершину, яка лежить найближче (з півплощини, де замітаюча пряма вже була) до першої (нерегулярної) вершини між ребрами, що лежать зліва та справа від нерегулярної вершини. Область пошуку другої вершини для першого проходу зображена на малюнку 3.14 в.
Мал. 3.14 в. Кружечком позначено нерегулярну вершину, штрихом - нове ребро.
Наведені вище міркування дозволяють запропонувати алгоритм, у якому для замітаючої прямої встановлюється порядок ребер (для довільного набору ребер можна вказати таке y=const, що для будь-яких двох ребер можна сказати яке з них лівіше, а яке правіше, що робить можливим введення порядку на множині ребер. Ребро вважається меншим за інше, якщо можна вказати таку точку на ньому, що горизонтальна пряма, яка проходить через цю точку, перетинає інше ребро в точці, що лежить правіше на прямій, ніж перша точка). Статус замітаючої прямої буде містити не тільки ребра, що перетинаються прямою у поточній точці подій, а й найближчі точки між ребрами, що вже зустрічались як точки подій. Отже, статус буде мати такий вигляд:
| Найближча точка лівіше ребра1 |
Ребро1 |
Найближча точка між ребром1 і ребром2 |
Ребро2 |
Найближча точка правіше ребра2 |
Таким чином, щоб скорегувати нерегулярну вершину, достатньо визначити, куди вона потрапляє у статусі та з'єднати її з точкою, найближчою у відповідному регіоні.
Алгоритм регуляризації планарного графа.
Перший прохід.
point = points.begin();
Вставити у line_sweep всі вихідні ребра з point відповідно до порядку, введеним на ребрах так, що line_sweep буде мати вигляд
point|rib1|point|rib2|…|ribn|point,
де rib1 < rib2 < … < ribn;
for(++point; point != points.end(); ++point)
{
for(rib = point.bottom.begin(); rib != point.bottom.end(); ++rib)
line_sweep.erase(rib);
// при видаленні ребра з статусу поточної прямої
// відбувається також знищення зон зліва
// та справа від нього, замість яких утворюється
// одна, що містить point (кінець ребра)
if(point.bottom.size() == 0) // нерег. т. I роду
ribs.insert(Segment(<точка у line_sweep, яка знаходиться у тій же області, що й point>, point);
for(rib = point.top.begin(); rib != point.top.end(); ++rib)
line_sweep.insert(rib);
// при додаванні ребра до статусу прямої замість
// зони, куди поптрапляє ребро, утворюються
// дві нові, що будуть лежати лівіше та
// правіше від ребра, яким присвоюється значення
// point (початок ребра)
}
Другий прохід (зверху донизу) робиться аналогічно.
На малюнку 3.15 показано регуляризований граф.
Аналіз. Під час роботи алгоритму кожне ребро буде точно один раз додаватись та вилучатись із статусу замітаючої прямої, який представлений збалансованим двійковим деревом пошуку. Отже, алгоритм потребує
O((n+m) * log(m)) часу та
O(m) пам'яті в гіршому випадку, який досягається коли всі ребра перетинаються однією горизонтальною прямою.
Теорема 3.9. N-вершинний плоский прямолінійний граф можна регуляризувати за час O(N log N) з витратою пам'яті O(N).
Мал. 3.15. Регуляризований плоский прямолінійний граф.
Попередня обробка. Припустимо, що ППЛГ заданий у вигляді структури даних РСПЗ. Побудова множин
IN(v) і
OUT(v) - О(N). Процедура балансування за вагою -
O(N). Регуляризація -
O(N log N) часу, отже час попередньої обробки займає
O(N log N).
Теорема 3.10. Локалізацію точки в N-вершинному планарному підрозбитті можна реалізувати методом ланцюгів за час O(log2 N) з використанням O(N) пам'яті при витратах O(N log N) часу на попередню обробку.

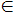 G;
G;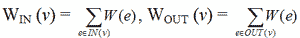
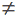 1, N) WIN (vj) = WOUT (vj).
1, N) WIN (vj) = WOUT (vj).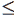 WOUT (vi) для всіх некрайніх vi. При другому проході від vN до v1 отримаємо WIN (vi)
WOUT (vi) для всіх некрайніх vi. При другому проході від vN до v1 отримаємо WIN (vi) 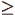 WOUT (vi). Отже після двох проходів матимемо реалізацію умови WIN (vi) = WOUT (vi). Позначимо vIN (v) = | IN(v)|, vOUT (v) = | OUT(v)|.
WOUT (vi). Отже після двох проходів матимемо реалізацію умови WIN (vi) = WOUT (vi). Позначимо vIN (v) = | IN(v)|, vOUT (v) = | OUT(v)|.