| Попередня | Змiст | Наступна |


{Ø} |
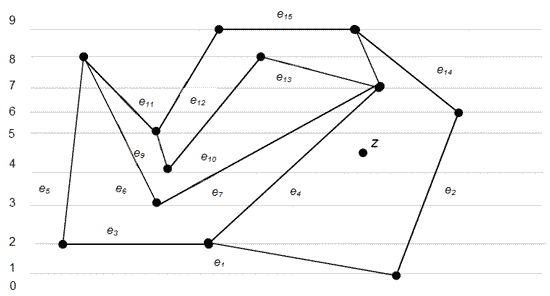
{e1, e2} |
{ e2, e3, e4, e5}{ e2, e4, e5, e6, e7 } |
{ e2, e4, e5, e6, e7, e9, e10} |
|
вст. |
вст. |
вст. |
вст. |
вст. |
{Ø} |
{e1, e2} |
{ e3, e4, e5} |
{ e6, e7 } |
{ e6, e7 } |
вил. |
вил. |
вил. |
вил. |
вил. |
{Ø} |
{Ø} |
{e1 } |
{e3 } |
{Ø} |
| Попередня | Змiст | Наступна |