3.3.3. Метод деталізації тріангуляції
Означення 3.11 Тріангуляція на множині вершин V на площині є плоским прямолінійним графом з максимальним числом ребер, що не перевищує 3| V | - 6 (за формулою Ейлера).
Нехай задана N-вершинна тріангуляція
G. Вважатимемо, що будується послідовність тріангуляцій
S1, S2, ... , Sh(N), S1= G, а Si отримується з Si-1 за такими правилами:
Крок (1). Вилучимо деяку максимальну множину несуміжних неграничних вершин Si-1 і інцендентні їм ребра.
Крок (2). Тріангулюємо многокутники, які утворились в результаті вилучення вершин та ребер.
Таким чином Sh(N) не має внутрішніх вершин.
Усі тріангуляції S1, S2, ..., Sh(N) мають одну загальну границю, оскільки на кроці (1) ми вилучали лише внутрішні вершини. Трикутники будемо позначати літерою R з індексами. Трикутник Rj може з'явитися в багатьох тріангуляціях, але Rj належить тріангуляції Si (позначимо Rj  * Si), якщо Rj створений на кроці (2) при побудові Si.
* Si), якщо Rj створений на кроці (2) при побудові Si.
Структура Т, топологію якої визначає направлений ациклічний граф, визначається наступним чином: від трикутника Rk до трикутника Rj проводиться дуга, якщо при побудові Si після Si-1 ми маємо:
- Rj вилучається з Si-1 на кроці (1);
- Rk створюється в Si на кроці (2);
- Rj
 Rk
Rk 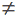 Ø.
Ø.
Критерій вибору вершин. Локалізація точки заданим методом буде найшвидшою у випадку пошукового дерева найменшої висоти. Щоб досягти цього, необхідно на кожному кроці вилучати максимально можливу множину несуміжних вершин із максимальним ступенем. Для великої кількості точок можна запропонувати наступний підхід щодо вибору та вилучення множини точок: починаючи з довільної вершини, помічаємо її сусідів (які не можуть вилучатися на поточному кроці) і продовжуємо доти, поки ще є непомічені сусіди.
Вважатимемо, що можна вибрати множину так, щоб виконувались наступні властивості (через Ni позначено число вершин в Si):
Властивість 1. Ni = aiNi-1, де aі 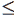 a < 1 для і = 2, ... , h(N).
a < 1 для і = 2, ... , h(N).
Властивість 2. Кожний трикутник Rj 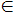 Si перетинається не більше ніж з H трикутниками з Si-1, і навпаки.
Si перетинається не більше ніж з H трикутниками з Si-1, і навпаки.
З властивості 1 ==> наслідок, що 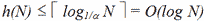 , оскільки при переході від Si-1 до Si вилучається фіксована доля вершин. Із властивостей 1 та 2 випливає, що пам'ять для Т рівна O(N). Ця пам'ять використовується для збереження вузлів і вказівників на їх нащадків. З теореми Ейлера про плоскі графи випливає, що Si містить Fi < 2Ni трикутників. Число вузлів Т, які представляють трикутники із Si, не перевищує Fi. Звідси випливає, що загальне число вузлів Т меньше, ніж
, оскільки при переході від Si-1 до Si вилучається фіксована доля вершин. Із властивостей 1 та 2 випливає, що пам'ять для Т рівна O(N). Ця пам'ять використовується для збереження вузлів і вказівників на їх нащадків. З теореми Ейлера про плоскі графи випливає, що Si містить Fi < 2Ni трикутників. Число вузлів Т, які представляють трикутники із Si, не перевищує Fi. Звідси випливає, що загальне число вузлів Т меньше, ніж
Щодо пам'яті для вказівників: за властивістю 2 кожен вузол має 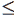 H вказівників ==>
H вказівників ==> 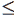 2NH / (1 - a) вказівників з'явиться в Т.
2NH / (1 - a) вказівників з'явиться в Т.
Теорема 3.11. Локалізацію точки в N-вершинному планарному підрозбитті методом деталізації тріангуляції можна зробити за час O(log N) з використанням O(N) пам'яті, якщо O(N log N) часу пішло на попередню обробку.
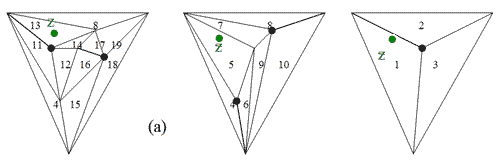
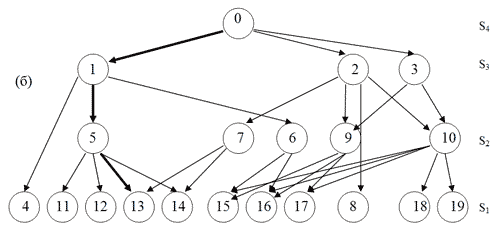
Приклад.
Мал. 3.19. Послідовність тріангуляцій ( а ) і відповідний їй направлений граф пошуку ( б ).
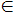 * Si
* Si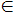 * Si), якщо Rj створений на кроці (2) при побудові Si.
* Si), якщо Rj створений на кроці (2) при побудові Si.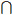 Rk
Rk 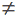 Ø.
Ø.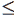 a < 1 для і = 2, ... , h(N).
a < 1 для і = 2, ... , h(N).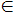 Si перетинається не більше ніж з H трикутниками з Si-1, і навпаки.
Si перетинається не більше ніж з H трикутниками з Si-1, і навпаки.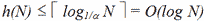 , оскільки при переході від Si-1 до Si вилучається фіксована доля вершин. Із властивостей 1 та 2 випливає, що пам'ять для Т рівна O(N). Ця пам'ять використовується для збереження вузлів і вказівників на їх нащадків. З теореми Ейлера про плоскі графи випливає, що Si містить Fi < 2Ni трикутників. Число вузлів Т, які представляють трикутники із Si, не перевищує Fi. Звідси випливає, що загальне число вузлів Т меньше, ніж
, оскільки при переході від Si-1 до Si вилучається фіксована доля вершин. Із властивостей 1 та 2 випливає, що пам'ять для Т рівна O(N). Ця пам'ять використовується для збереження вузлів і вказівників на їх нащадків. З теореми Ейлера про плоскі графи випливає, що Si містить Fi < 2Ni трикутників. Число вузлів Т, які представляють трикутники із Si, не перевищує Fi. Звідси випливає, що загальне число вузлів Т меньше, ніж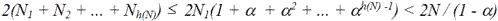
 H вказівників ==>
H вказівників ==> 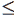 2NH / (1 - a) вказівників з'явиться в Т.
2NH / (1 - a) вказівників з'явиться в Т.