5.3. Найближча пара - метод "розподіляй та володарюй".
Нижня оцінка задачі "найближча пара" має складність
Ω(Nlog N). Для побудови алгоритмів з такою оцінкою є два шляхи:
безпосереднє використання сортування і використання метода "розподіляй та володарюй".
Перший підхід можна відразу відкинути, так як сортування
зручне лише в умовах повної впорядкованості, яка полягає у проектуванні усіх точок
на деяку пряму, але при цьому втрачається суттєва в даному випадку інформація.
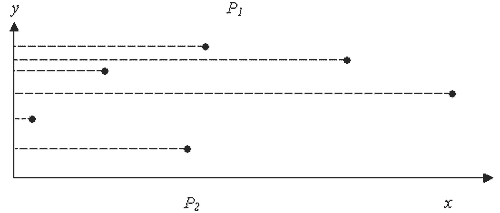
Це демонструє малюнок 5.7, на якому точки р1, р2 утворюють найближчу пару, але при цьому дають максимальну відстань при проектуванні на вісь y.
Мал. 5.7. Точки р1 і р2, які утворюють найближчу пару мають найбільшу відстань по y-координаті.
Другий шлях для досягнення складності
Ω(Nlog N) полягає в розбитті задачі на дві підзадачі, розв'язок яких можна об'єднати за лінійний час, отримавши рішення вихідної задачі. Позначивши через P(N, 2) час роботи алгоритму, який шукає найближчу пару точок на площині, отримаємо рекурентне співвідношення:
| P(N, 2) = 2P(N/2, 2) + O(N2) | (5.1) |
Розв'язком цього співвідношення є P(N, 2) = O(N2), що не дає бажану оцінку.
Алгоритм "розподіляй та володарюй"
Одновимірний випадок. Алгоритм впорядковує
точки множини, а потім проглядає її за лінійний час.
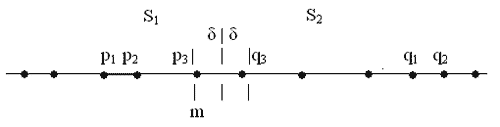
Мал.5.8. Метод "розподіляй та володарюй" в одновимірному випадку.
Нехай точка m розбиває множину на дві
підмножини S1 та S2 і
при цьому p < q для всіх p 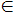 S1 i
q
S1 i
q 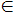 S2.
Розв'язавши окремо рекурсивно задачу про найближчу пару для множин
S1 та S2, отримаємо
дві найближчі пари точок {p1, p2} i
{q1, q2} відповідно.
Нехай δ1 = min(S1)=
| p2 - p1 | і
d2 = min (S2)=| q2 - q1 | -
відстані для знайдених пар відповідно. Позначимо через
δ найменшу серед знайдених
δ1 і δ2 відстаней:
S2.
Розв'язавши окремо рекурсивно задачу про найближчу пару для множин
S1 та S2, отримаємо
дві найближчі пари точок {p1, p2} i
{q1, q2} відповідно.
Нехай δ1 = min(S1)=
| p2 - p1 | і
d2 = min (S2)=| q2 - q1 | -
відстані для знайдених пар відповідно. Позначимо через
δ найменшу серед знайдених
δ1 і δ2 відстаней:
| δ = min (δ1, δ2) = min(δ| p2 - p1 |, | q2 - q1 |) | (5.2) |
Найближчою парою є {p1, p2}
або {q1, q2}, або {p3, q3},
де р3 = max(S1),
q3 = min(S2).
Для того щоб відстань, яку визначає пара
{p3, q3}, була менше δ,
p3 i q3 повинні бути
на відстані, яка не перевищує δ від точки m
(|p3 - q3| < δ 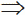 |p3 - m| < δ або |q3 - m| < δ) .
Відкладемо ліворуч і праворуч відносно точки m відрізки довжиною δ.
|p3 - m| < δ або |q3 - m| < δ) .
Відкладемо ліворуч і праворуч відносно точки m відрізки довжиною δ.
Скільки ж точок множини S1
можуть міститись в інтервалі (m - δ, m]?
Так як кожен напіввідкритий інтервал довжиною δ містить не більше однієї точки
множини S1, то інтервал
(m - δ, m] містить не більше однієї точки.
Аналогічно інтервал [m, m + δ).
Очевидно, що усі точки, які потрапляють в інтервали (m - δ, m]
та [m, m + δ), можна визначити, переглянувши множину за
лінійний час. Отже визначивши
dist(max(S1), min(S2)) = |p3 - q3|,
знайдемо остаточно
| δ* = min(δ(S1), δ(S2), dist(max(S1), min(S2))) = min(| p2 - p1|, |q2 - q1|, |p3 - q3|) | (5.3) |
а значить і найближчу пару точок. Таким чином отримаємо наступний алгоритм зі складністю O(N log N).
Двовимірний випадок.
Узагальнення на двовимірний випадок можна виконати безпосередньо.
Розіб'ємо множину точок на площині S на дві підмножини
S1 і S2
вертикальною прямою l ,
яка є медіаною множини S за x-координатою так,
щоб кожна точка множини S1 лежала лівіше
будь-якої точки S2.
Розв'язавши рекурсивно задачу для S1 і
S2, одержимо числа
δ1, δ2 -
мінімальні відстані для множин S1 і
S2 відповідно.
Покладемо δ = min(δ1, δ2).
Якщо найближчу пару утворюють точки
р 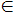 S1 і
q
S1 і
q 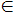 S2, то відстань від
точок q і p до
l не перевищує δ.
Позначимо через Р1 і Р2
вертикальні смуги шириною δ, розташовані відповідно ліворуч та
праворуч від l, то р
S2, то відстань від
точок q і p до
l не перевищує δ.
Позначимо через Р1 і Р2
вертикальні смуги шириною δ, розташовані відповідно ліворуч та
праворуч від l, то р 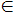 S1 і q
S1 і q 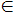 S2, мал. 5.9.
S2, мал. 5.9.
Мал. 5.9. Метод "розподіляй та володарюй" у випадку площини.
На прямій було не більше одного кандидата для
q і p.
У процедурі БПАРА1 є точно один кандидат для р:
р = max(S1). На площині таким кандидатом може бути будь-яка
точка, якщо вона знаходиться на відстані не більшій за δ
від прямої l. На мал. 5.10 наведено приклад такої множини.
Мал. 5.10. Усі точки можуть знаходитсь на відстані, яка не перевищує δ від прямої l.
Мал. 5.11. Для кожної точки із Р1 необхідно перевірити не більше шести точок із Р2.
Розглянемо в смузі Р1
довільну точку р. Необхідно знайти усі точки q
із Р2, які віддалені від p не
більше ніж на δ. Усі вони розташовуються у прямокутнику
R розміром δ × 2δ.
Максимальна кількість точок, які можна помістити в такий прямокутник так,
щоб відстань між ними була не менша за δ, рівна 6.
Це означає, що для кожної точки із Р1 необхідно
досліджувати лише не більше 6 точок із Р2.
Тому на кроці злиття розв'язків підзадач необхідно виконати не більше 6
× N / 2 = 3N порівнянь у порівнянні з N 2/ 4.
Спроектуємо точку р і усі точки із
Р2 на пряму l.
Для визначення точок із Р2, які потрапили в
R, можна розглянути лише проекції точок, які знаходяться на відстані не більшій
за δ від проекції точки р.
Якщо точки впорядковані за у-координатою, то для усіх точок із Р1 "кандидати" на місце їх найближчого сусіда із Р2 визначаються за один прохід впорядкованого списку.
procedure НПАРА2(S)
- розбити S на дві підмножини S1 та S2 вертикальною прямою l (медіаною).
- Рекурсивно знайти відстань для найближчих пар δ1 та δ2.
- δ := min (δ1, δ2).
- Нехай Р1 - множина точок із S1, які лежать в смузі на відстані δ від розділяючої прямої l, а Р2 - аналогічна підмножина в S2.
Спроектувати Р1 та Р2
на l та впорядкувати проекції за у-координатою.
Нехай Р1* та Р2* -
відповідні впорядковані послідовності.
- "Злиття" можна виконати переглядом кожної точки з Р1*,
вивчаючи точки з Р2*, які знаходяться на відстані, що не перевищує δ.
Поки вказівник просувається послідовністю Р1*,
вказівник на Р2* переміщується вперед-назад,
залишаючись в інтервалі шириною 2δ .
Нехай δ1 - мінімальна відстань між парою точок.
- δS := min(δ, δl).
Якщо позначити через Т(N) час обробки
алгоритмом множини із N точок, то час, який пішов на обробку на
кроці 1 та 5 дорівнює O(N), на кроці 3 та 6 - О(1),
а крок 2 потребує часу 2T(N/2).
Скориставшись попереднім сортуванням для часу обробки P(N, 2)
алгоритму пошуку найближчої пари, отримаємо співвідношення:
| P(N, 2) = 2P(N/2, 2) + O(N) = O(N log N) | (5.5) |
На основі співвідношення маємо теорему:
Теорема 5.4. Найкоротша відстань,
яка визначається N точками на площині, може бути знайдена за час
θ(N log N) і є оптимальна.
function НПАРА1(S)
begin if (|S| = 2) then δ := | X[2] - X[1] |
else if (|S| = 1) then δ := ∞
else begin m:= Медіана(S);
Побудувати (S1, S2) (*S1 = {p: p 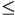 m}, S2 = {p: p > m}*);
δ1 := НПАРА(S1);
δ2 := НПАРА(S2);
p := max (S1);
q := min (S2);
δ := min (δ1, δ2, q - p)
end;
return δ
end.
m}, S2 = {p: p > m}*);
δ1 := НПАРА(S1);
δ2 := НПАРА(S2);
p := max (S1);
q := min (S2);
δ := min (δ1, δ2, q - p)
end;
return δ
end.

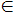 S1 i
q
S1 i
q 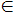 S2.
Розв'язавши окремо рекурсивно задачу про найближчу пару для множин
S1 та S2, отримаємо
дві найближчі пари точок {p1, p2} i
{q1, q2} відповідно.
Нехай δ1 = min(S1)=
| p2 - p1 | і
d2 = min (S2)=| q2 - q1 | -
відстані для знайдених пар відповідно. Позначимо через
δ найменшу серед знайдених
δ1 і δ2 відстаней:
S2.
Розв'язавши окремо рекурсивно задачу про найближчу пару для множин
S1 та S2, отримаємо
дві найближчі пари точок {p1, p2} i
{q1, q2} відповідно.
Нехай δ1 = min(S1)=
| p2 - p1 | і
d2 = min (S2)=| q2 - q1 | -
відстані для знайдених пар відповідно. Позначимо через
δ найменшу серед знайдених
δ1 і δ2 відстаней: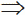 |p3 - m| < δ або |q3 - m| < δ) .
Відкладемо ліворуч і праворуч відносно точки m відрізки довжиною δ.
|p3 - m| < δ або |q3 - m| < δ) .
Відкладемо ліворуч і праворуч відносно точки m відрізки довжиною δ.
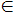 S1 і
q
S1 і
q 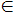 S2, то відстань від
точок q і p до
l не перевищує δ.
Позначимо через Р1 і Р2
вертикальні смуги шириною δ, розташовані відповідно ліворуч та
праворуч від l, то р
S2, то відстань від
точок q і p до
l не перевищує δ.
Позначимо через Р1 і Р2
вертикальні смуги шириною δ, розташовані відповідно ліворуч та
праворуч від l, то р 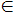 S1 і q
S1 і q 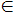 S2, мал. 5.9.
S2, мал. 5.9.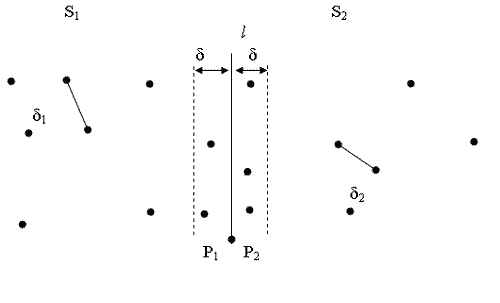

m}, S2 = {p: p > m}*); δ1 := НПАРА(S1); δ2 := НПАРА(S2); p := max (S1); q := min (S2); δ := min (δ1, δ2, q - p) end; return δ end.