ГЛАВА 5. БЛИЗКІСТЬ. ОСНОВНІ АЛГОРИТМИ.
5.1. Основні задачі.
Почнемо з перерахування різних, на перший погляд задач, які відносяться до визначення близькості, але які, близькі з точки зору процедури їх розв'язання.
Задача Б.1 (НАЙБЛИЖЧА ПАРА). На площині задано N точок. Знайти дві із них, відстань між якими найменша (може виявитись, що таких пар може бути декілька, тоді достатньо знайти хоча б одну із них).
Ця задача настільки просто формулюється і настільки важлива, що її можна розглядати як одне із основних питань обчислювальної геометрії як з точки зору її застосувань, так і з суто теоретичної точки зору. Наприклад, одне із застосувань цієї задачі стосується системи реального часу, яка керує рухом літаків: з деякими спрощеннями можна вважати, що на найбільшу небезпеку зіткнення наражаються два літаки, відстань між якими найменша.
Центральне питання розробки алгоритму розв'язання цієї задачі полягає в тому, чи обов'язковим є перебір кожної пари точок, щоб знайти мінімальну відстань.Звичайний перебір кожної пари точок у випадку d- вимірного простору дає час О(dN2).
В одновимірному випадку існує більш швидкий алгоритм, який використовує той факт, що кожна пара найближчих точок повинна складатись із послідовних точок множини при упорядкуванні її за значенням координати. Таким чином можна упорядкувати N заданих дійсних чисел за О(N log N) кроків, а потім здійснити лінійний перегляд упорядкованої послідовності (x1, x2, …, xN ) за час О(N), обчислюючи при цьому xi+1- xi, і=1,...,N-1.
Задача Б.2 (УСІ НАЙБЛИЖЧІ СУСІДИ). На площині задано N точок. Знайти найближчого сусіда для кожної точки множини.
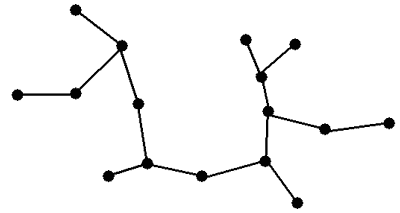
Означення 5.1. "Найближчий сусід" - це відношення на множині точок S, яке визначається таким чином: точка b є найближчим сусідом точки a (позначається a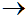 b), якщо
b), якщо
dist(a,b) = mindist(a,c), c 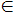 S - a.
S - a.
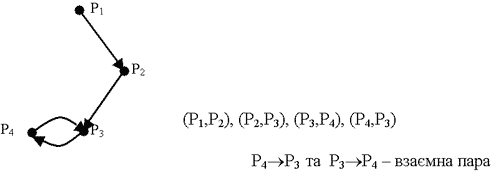
Мал. 5.1. Граф відношення "Найближчий сусід" на множині точок.
Відношення необов'язково симетричне (Із того, що a 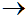 b не обов'язково
b не обов'язково 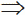 b
b 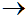 a). (Хоча точка може мати найближчим сусідом кожну із точок множини, вона може, бути найближчим сусідом не більше 6 точок для d = 2 і не більше 12 для d = 3). Розв'язком задачі є сукупність упорядкованих пар (a,b), де a
a). (Хоча точка може мати найближчим сусідом кожну із точок множини, вона може, бути найближчим сусідом не більше 6 точок для d = 2 і не більше 12 для d = 3). Розв'язком задачі є сукупність упорядкованих пар (a,b), де a 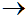 b.
b.
Означення 5.2 Пара точок, яка задовольняє умову симетричності відношення, називається взаємною парою.
Задача Б.3 (ЕВКЛІДОВЕ МІНІМАЛЬНЕ КІСТЯКОВЕ ДЕРЕВО). На площині задано N точок. Побудувати дерево, вершинами якого є усі задані точки і сумарна довжина усіх ребер якого мінімальна.
Розв'язком задачі є список, який містить N-1 пару точок. Кожна пара представляє ребро дерева. На малюнку 5.2 показаний приклад такого дерева.
Мал. 5.2. Мінімальне кістякове дерево множини точок на площині.
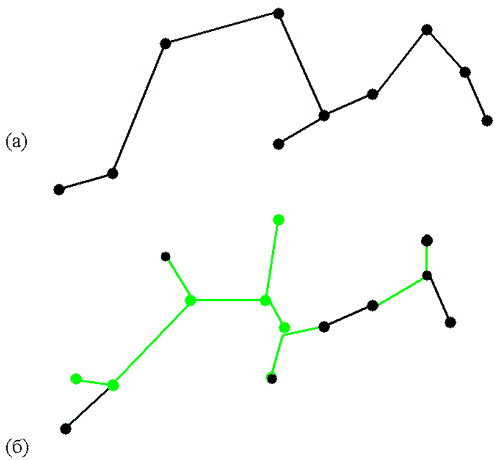
Означення 5.3 Дерево, яке має найкоротшу довжину і задовольняє умову, що до вихідної множини не заборонено додавати нові точки, називається деревом Штейнера (мал. 5.3).
Задача про МКД зазвичай формулюється як задача теорії графів:
задано зважений граф з N вершинами і E ребрами,
необхідно знайти найкоротше піддерево графа G,
яке містить усі його вершини.
У випадку евклідової задачі про МКД N вершин
визначаються 2N координатами точок на площині,
а відповідний граф містить ребра, які з'єднують кожну пару вершин.
Вага ребра дорівнює відстані між точками, з'єднаних ребром.
У цьому випадку використання кращого із відомих алгоритмів розв'язання задачі про МКД
вимагатиме часу q(N2).
Таким чином МКД завжди містить найкоротше ребро графа G, наведене значення є нижньою оцінкою для довільного графа.
Мал. 5.3. Сумарна довжина ребер дерева Штейнера (б) може бути меншою, ніж у МКД.
Задача Б.4 (ТРІАНГУЛЯЦІЯ). На площині задано N точок. З'єднати їх відрізками, що не перетинаються, таким чином, щоб кожна область всередині опуклої оболонки цієї множини точок була б трикутником.
Граф тріангуляції множини із N точок,
будучи планарним, має не більше 3N - 6 ребер.
Результатом розв'язання сформульованої вище задачі має бути принаймні список цих ребер.
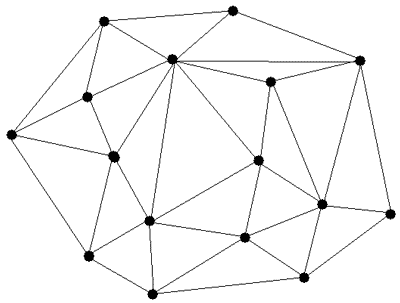
Приклад тріангуляції наведено на мал.5.4.
Мал. 5.4. Тріангуляція множини точок.
Задача тріангуляції виникає у методі скінчених елементів [8]
і при інтерполяції функції від двох змінних,
якщо задані значення функції в N довільним чином розташованих точках
(xi, yi ) і вимагається апроксимувати її
в деякій новій точці (x, y). Один із можливих підходів базується
на кусково-лінійній інтерполяції, при якій поверхня, яка визначається функцією,
апроксимується "сіткою", яка складається із плоских трикутних граней.
Проекція кожної точки (x, y) належить лише одній із трикутних граней,
і відповідне значення функції f(x, y) обчислюється в результаті
визначення інтерполюючої площини, яка проходить через три вершини грані.
Процес тріангуляції полягає у виборі трьох точок, які і будуть утворювати грані.
Для визначення "якості" тріангуляції, яка одержується, було запропоновано немало критеріїв [7],
які включають, зокрема, максимізацію найменшого кута або мінімізацію повної довжини ребер.
Вибір указаних умов пояснюється їх зручністю для одержання оцінки похибки інтерполяції,
а не тим, що вони дозволяють одержати найкращу тріангуляцію.
Усі чотири попередні задачі відносяться до задач,
розв'язок яких шукається лише один раз і полягає в побудові деякого геометричного об'єкту
( найближчої пари точок, усіх найближчих сусідів, ЕМКД і тріангуляції).
Розглянемо дві задачі пошуку, які необхідно розв'язувати багатократно і які, внаслідок цього,
допускають попередню доробку початкових даних.
Задача Б.5 (ПОШУК НАЙБЛИЖЧОГО СУСІДА).
На площині задано N точок. Як швидко можна знайти найближчого сусіда для деякої нової
точки q, за умови, що допускається попередня обробка?
У просторі розмірності d цю задачу можна
розв'язати за час О(dN).
Існує багато прикладних задач, в яких може бути використаний такий
швидкий пошук. Найважливішою з них є задача класифікації. Один із методів класифікації
базується на правилі найближчого сусіда [3,4].
Відповідно до цього правила, якщо необхідно класифікувати об'єкт на приналежність до одного
із заданих класів, то його слід віднести до класу, який відповідає його найближчому сусіду.
Схожа ситуація має місце в інформаційних системах при вибірці
інформації, коли вибирається запис, що найкращим чином відповідає запису-запиту [3].
У випадку, коли необхідно обробляти велику кількість об'єктів, розв'язуючи або задачі
класифікації [2] (при розпізнаванні мови, ідентифікації елементарних частинок і т.д.), або
задачі вибірки даних ( вибірка найбільш підходящого елементу), необхідно досить швидко
виконувати пошук найближчого сусіда.
Задача Б.6 (k-НАЙБЛИЖЧИХ СУСІДІВ).
На площині задано N точок. Як швидко можна знайти k - точок,
найближчих до деякої нової точки q, за умови,
що допускається попередня обробка?
Процедура пошуку k-найближчих сусідів
використовувалась при інтерполяції і виділені контурів [1], і при класифікації
(правило, яке використовує k найближчих сусідів, є більш стійким до
всякого типу випадковостей в порівнянні з тим, коли рішення приймається з
врахуванням лише єдиного сусіда).
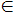 S - a.
S - a.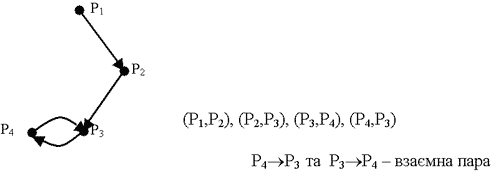
 b), якщо
b), якщо 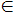 S - a.
S - a.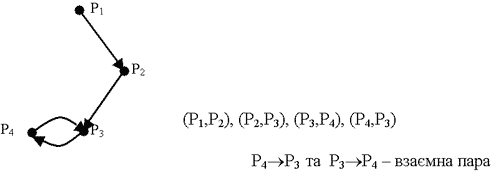
 b не обов'язково
b не обов'язково 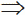 b
b 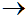 a). (Хоча точка може мати найближчим сусідом кожну із точок множини, вона може, бути найближчим сусідом не більше 6 точок для d = 2 і не більше 12 для d = 3). Розв'язком задачі є сукупність упорядкованих пар (a,b), де a
a). (Хоча точка може мати найближчим сусідом кожну із точок множини, вона може, бути найближчим сусідом не більше 6 точок для d = 2 і не більше 12 для d = 3). Розв'язком задачі є сукупність упорядкованих пар (a,b), де a 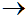 b.
b.