4.7. УЗАГАЛЬНЕННЯ:ПІДТРИМКА ДИНАМІЧНОЇ ОПУКЛОЇ ОБОЛОНКИ.
Метод Препарата можна розглядати як метод підтримки структури даних, що описує опуклу оболонку множини точок у випадку, коли допускається лише операція вставки точок. Постає питання, чи можна розробити структуру даних, яка організує множину точок на площині і описує їх поточну опуклу оболонку, в припущені, що допускаються не лише вставка, але й вилучення точки?
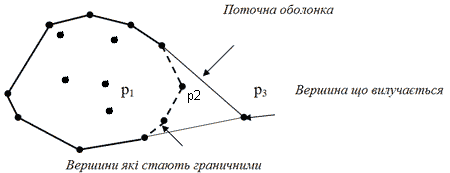
Відповідь на це питання непроста. У той час як у попередньому алгоритмі побудови ОО точки, які є внутрішніми для поточної опуклої оболонки, назавжди виключаються з розгляду, в даній ситуації необхідно організувати усі точки, що містяться на поточний момент у множині, так як вилучення деякої точки поточної опуклої оболонки може призвести до того, що деякі внутрішні точки стануть граничними точками нової опуклої оболонки ( мал. 4.15). Наведемо формальну постановку цієї задачі:
Задача ОО6. (ПІДТРИМКА ОБОЛОНКИ). Задані порожня множина S і послідовність із N точок (р1, р2, ..., рN ), кожна з яких або додається до множини S, або вилучається з неї. Необхідно підтримувати опуклу оболонку множини S.
Мал. 4.15. При вилучені точки р3 точки р1 і р2 стають граничними точками опуклої оболонки.
Використовується той факт, що границя опуклої оболонки є об'єднанням
двох (опуклих) монотонних ламаних ліній (ланцюгів), які обмежують оболонку зверху і знизу
і відповідно до цього називаються В-оболонкою і Н-оболонкою множини точок.
Розглянемо побудову В-оболонки.
Алгоритм
Відповідна структура даних організована наступним чином.
Її основою є збалансоване за висотою двійкове дерево пошуку Т,
листки якого використовуються для збереження точок поточної множини.
Процедура пошуку буде проводитися відповідно до значення абсциси точок, тобто проходження
листків дерева зліва направо дає множину точок, впорядковану за x-координатою.
Зазначимо, що послідовність точок В-оболонки ( її вершин) також впорядкована
за зростанням абсциси, і, тому вона є підпослідовністю глобальної послідовності точок,
яка зберігається в листках дерева. Упорядковуємо S за
x - координатою. Нехай v - вузол дерева
Т. Позначимо через ЛСИН[v] і
ПСИН[v] його лівого і правого нащадків відповідно.
Побудуємо В-оболонку точок, які зберігаються в листках піддерева з коренем
у вузлі v. Позначимо через U(v) В-оболонку множини точок, які зберігаються в листках
піддерева з коренем v. Виходячи із принципу індукції, припустимо, що вже існують U(ЛСИН[v]) і
U(ПСИН[v]). Далі (мал. 4.16) визначаються дві опорні точки
р1 і р2
єдиного спільного опорного відрізку для двох оболонок. Тут використовується функція
З'ЄДНАТИ(U1, U2),
яка дозволяє знайти опорний відрізок для двох В-оболонок
U1, U2.
Функція З'ЄДНАТИ дозволяє ефективно розчіпляти U1
на два ланцюги, які складають впорядковану пару (U11, U12),
і аналогично U2- на пару ланцюгів (U21, U22). При цьому виконується така умова: опорна точка р1  U1 входить до складу U11, а точка р2
U1 входить до складу U11, а точка р2  U2 - до складу U22 (тобто в обох випадках опорна точка належить "зовнішньому" підланцюгу). На цьому етапі, зчепивши U11 і U22, одержуємо шукану В-оболонку U1
U2 - до складу U22 (тобто в обох випадках опорна точка належить "зовнішньому" підланцюгу). На цьому етапі, зчепивши U11 і U22, одержуємо шукану В-оболонку U1  U2. Природно, щоб кожен вузол v дерева Т вказував на зчеплену чергу, яка представляє ту частину U(v), яка не належить U(БАТЬКО[v]).
U2. Природно, щоб кожен вузол v дерева Т вказував на зчеплену чергу, яка представляє ту частину U(v), яка не належить U(БАТЬКО[v]).
Обернена операція: маючи U(v), одержати U(ЛСИН[v]) і U(ПСИН[v]).
Знаючи ребро [р1, р2], яке з'єднує опорні точки (одне ціле число J[v], яке вказує на положення точки р1 у ланцюзі вершин U(v)), можна розчепити U(v) на ланцюги U11 і U22, які в свою чергу можуть бути зчеплені з ланцюгами, що зберігаються в ЛСИН[v] і ПСИН[v] відповідно. Структура даних Т доповнюється такими атрибутами, які пов'язуються з кожним вузлом v дерева:
- Вказівником на зчеплену чергу Q[v], яка містить частину U(v), що не входить до U(БАТЬКО[v]) ( якщо v є коренем, то Q[v]=U(v) ).
- Цілим числом J[v], яке вказує на положення (індекс) лівої опорної точки в U(v).
Мал. 4.16. Для побудови В-оболонки об'єднання оболонок U1 і U2 будується спільний опорний відрізок (міст) [p1,p2].
Функція З'ЄДНАТИ(U1, U2):
- Знайти р1 і р2.
- Розчепити U1 на U11 та U12.
- Розчепити U2 на U21 та U22.
- Зчепити U11 з U22
 CH(S1
CH(S1 S2): U11*U22
S2): U11*U22
Структура даних використовує пам'ять об'ємом О(N).
Враховуючи, що операції розчеплення і зчеплення зчеплених черг є стандартними, наша увага буде зосереджена на операції, що виконується функцією З'ЄДНАТИ, для якої був запропонований наступний розв'язок:
Лема 4.1. З'єднання двох розділених опуклих ланцюгів, які містять в сумі N точок, може бути виконане за О(logN) кроків.
Доведення. Нехай дано дві В-оболонки U1, U2 і дві вершини q1 U1, q2
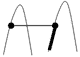
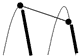
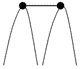
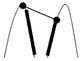
U1, q2 U2. Кожна із цих двох вершин може бути класифікована відносно відрізка [q1,q2] як опукла, опорна або ввігнута. Залежно від класифікації можливі 9 випадків, схематично зображених на малюнку 4.17(а). Усі випадки зрозумілі за винятком випадку (q1,q2) = (ввігнута, ввігнута), який детальніше представлений на малюнку 4.17 (б).
Нехай пряма l1 проходить через
q1 і її правого сусіда на U1.
Аналогічно пряма l2 проходить через
q2 і її лівого сусіда на U2.
Позначимо через р точку перетину прямих l1 і l2.
U1 і U2 розділимі вертикаллю l.
U2. Кожна із цих двох вершин може бути класифікована відносно відрізка [q1,q2] як опукла, опорна або ввігнута. Залежно від класифікації можливі 9 випадків, схематично зображених на малюнку 4.17(а). Усі випадки зрозумілі за винятком випадку (q1,q2) = (ввігнута, ввігнута), який детальніше представлений на малюнку 4.17 (б).
Нехай пряма l1 проходить через
q1 і її правого сусіда на U1.
Аналогічно пряма l2 проходить через
q2 і її лівого сусіда на U2.
Позначимо через р точку перетину прямих l1 і l2.
U1 і U2 розділимі вертикаллю l.
1. Припустимо, що точка р знаходиться праворуч від
прямої l. р1 може належати лише
заштрихованій області і u(y) < v(y)
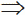 довільна вершина q"
довільна вершина q"  U2прав. відносно q2,
є ввігнутою відносно відрізка [q',q"],
де q'- довільна вершина U1 і U2прав. відносно q2 не розглядається.
Що стосується ланцюга ліворуч від вершини q1,
то для нього не можна це стверджувати.
U2прав. відносно q2,
є ввігнутою відносно відрізка [q',q"],
де q'- довільна вершина U1 і U2прав. відносно q2 не розглядається.
Що стосується ланцюга ліворуч від вершини q1,
то для нього не можна це стверджувати.
2. Якщо точка перетину р знаходиться ліворуч від прямої
l, то ланцюг ліворуч від вершини
q1 можна не розглядати.
( а )
| q2\q1 |
ввігнута |
опорна |
опукла |
| ввігнута |
 |
 |
 |
| опорна |
 |
 |
 |
| опукла |
 |
 |
 |
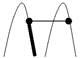
Мал. 4.17 (а). Усі можливі випадки, які виникають при виборі деякої вершини з U1 і деякої вершини з U2
|
T(U1) |
T(U1) |
| 0 |
v(q1) |
v(q2) |
| 1 |
v(q1) (або ПС[v(q1)]) |
ЛС[v(q2)] (або v(q2)) |
| 2 |
ПС[v(q1)] |
ПС [v(q2)] |
| 3 |
v(q1) |
ПС [v(q2)] |
| 4 |
ЛС [v(q1)] |
ЛС [v(q2)] |
| 5 |
Результат |
Результат |
| 6 |
ЛС [v(q1)] |
ПС [v(q2)] |
| 7 |
ЛС [v(q1)] |
v(q2) |
| 8 |
ЛС [v(q1)] |
ПС [v(q2)] |
| 9 |
ЛС [v(q1)] |
ПС [v(q2)] |
( б )
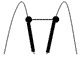
Мал. 4.17 (б). Ілюстрація випадку (ввігнута, ввігнута).
Якщо цей процес починається з кореневих вершин обох дерев, які представляють U1 і U2 відповідно, то із збалансованості цих дерев випливає, що час виконання функції З'ЄДНАТИ(U1, U2) складає О(logN), де N - це, зазвичай, сумарне число вершин у двох оболонках.
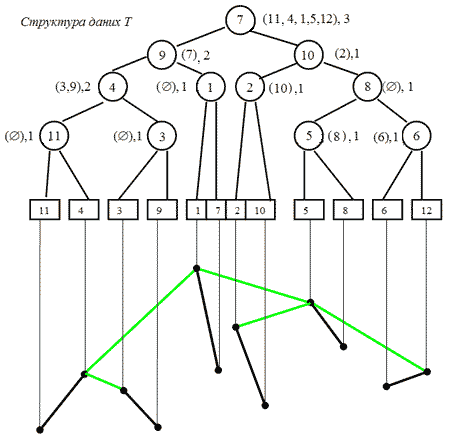
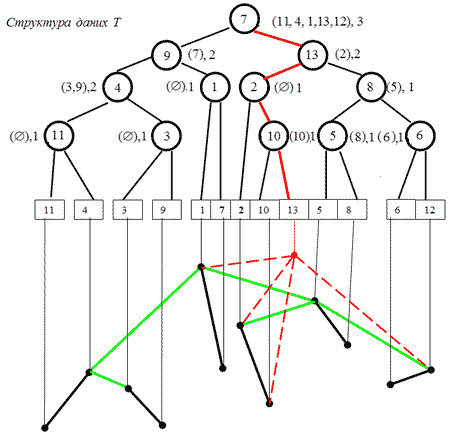
Маючи функцію З'ЄДНАТИ, можна аналізувати процес динамічної підтримки опуклої оболонки на площині, мал. 4.18. Номери точок відповідають порядку, в якому вони додавалися до множини. В структурі даних Т кожний лист відповідає точці, кожний нелистовий вузол - мосту ( тобто опорному відрізку, який з'єднує дві оболонки). Для кожного такого вузла вказана пара Q[v], J[v]. Структура даних описує деяке дерево оболонки.
Розглянемо вставку нової точки р13. Процедура вставки повинна не лише підтримувати збалансоване за висотою дерево Т, використовуючи для цього звичайний метод балансування [4,5], але й робити все необхідне для того, щоб зчеплена черга, пов'язана з кожною вершиною, задовольняла вимоги, вказані у визначенні структури даних Т.
Мал. 4.18. Множина точок на площині і відповідна їй структура даних Т.
Припустимо для простоти, що балансування не потрібне ( усі дії з балансування просто збільшують число вузлів, які необхідно обробляти, не приводячи до будь-яких принципових відмінностей). Тому будемо вважати, що точка р13 додається до множини точок, представленої на малюнку 4.18, як це показано на малюнку 4.19. На цьому малюнку показано також стан структури даних Т після вставки точки р13. Зазначимо, що р13 однозначно визначає шлях із кореня дерева Т до листа, в якому повинна бути вставлена р13. Рухаючись по цьому шляху із кореня, в кожному вузлі, який знаходиться на цьому шляху, ми складаємо В-оболонку , яка відноситься до цього вузла, і потім, використовуючи параметр J[v], розбиваємо її на частини, щоб передати двом нащадкам цього вузла відповідні їм частини.
Мал. 4.19. Вставка точки р13. При вставці зачеплені вузли: {(11,4,1,13,12), 3}, {(2),2}, {( ),1}, {(5), 1}, {(10),1}, {13}
Більш формально спуск по дереву з метою вставки точки р здійснюється шляхом виклику рекурсивної процедури СПУСК(v,p):
procedura СПУСК(v,p)
begin if (v
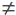
лист)
then
begin (QL,QR):= РОЗЧЕПИТИ(U[v], J[v])
U[ЛСИН[v]]:= ЗЧЕПИТИ(QL,Q[ЛСИН[v]]);
U[ПСИН[v]]:= ЗЧЕПИТИ(Q[ПСИН[v]],QR);
if (x[p]
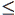
x[v])
then v:= ЛСИН[v]
else v:= ПСИН[v];
СПУСК(v,p)
end
end.
Підйом по дереву здійснюється за допомогою наступної процедури:
procedura ПІДЙОМ(v)
begin if (v
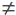
корінь)
then
begin (Q1, Q2, Q3, Q4, J):= З'ЄДНАТИ(U[v], U[БРАТ[v]]);
Q[ЛСИН[БАТЬКО[v]]]:= Q2;
Q[ПСИН[БАТЬКО[v]]]:= Q3;
U[БАТЬКО[v]]:= ЗЧЕПИТИ(Q1,Q4);
J[БАТЬКО[v]]:= J;
ПІДЙОМ(БАТЬКО[v])
end
else Q[v]:= U[v]
end.
Так як k 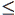 N, то час обробки одного вузла у процедурі СПУСК дорівнює O(logN). А так як глибина дерева Т також рівна O(logN), то час виконання процедури СПУСК дорівнює O(log2N) у гіршому випадку. Процедура ПІДЙОМ дає час O(logN).
N, то час обробки одного вузла у процедурі СПУСК дорівнює O(logN). А так як глибина дерева Т також рівна O(logN), то час виконання процедури СПУСК дорівнює O(log2N) у гіршому випадку. Процедура ПІДЙОМ дає час O(logN).
Теорема 4.11 Динамічна підтримка В-оболонки і Н-оболонки з N точок на площині може бути виконана з часовими витратами на операції вставки і вилучення, що дорівнюють O(log2N) в гіршому випадку.

 U1 входить до складу U11, а точка р2
U1 входить до складу U11, а точка р2  U2 - до складу U22 (тобто в обох випадках опорна точка належить "зовнішньому" підланцюгу). На цьому етапі, зчепивши U11 і U22, одержуємо шукану В-оболонку U1
U2 - до складу U22 (тобто в обох випадках опорна точка належить "зовнішньому" підланцюгу). На цьому етапі, зчепивши U11 і U22, одержуємо шукану В-оболонку U1  U2. Природно, щоб кожен вузол v дерева Т вказував на зчеплену чергу, яка представляє ту частину U(v), яка не належить U(БАТЬКО[v]).
U2. Природно, щоб кожен вузол v дерева Т вказував на зчеплену чергу, яка представляє ту частину U(v), яка не належить U(БАТЬКО[v]).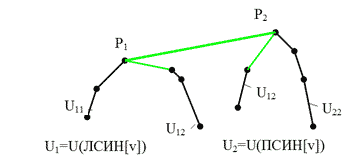
 CH(S1
CH(S1 S2): U11*U22
S2): U11*U22 U1, q2
U1, q2 U2. Кожна із цих двох вершин може бути класифікована відносно відрізка [q1,q2] як опукла, опорна або ввігнута. Залежно від класифікації можливі 9 випадків, схематично зображених на малюнку 4.17(а). Усі випадки зрозумілі за винятком випадку (q1,q2) = (ввігнута, ввігнута), який детальніше представлений на малюнку 4.17 (б).
Нехай пряма l1 проходить через
q1 і її правого сусіда на U1.
Аналогічно пряма l2 проходить через
q2 і її лівого сусіда на U2.
Позначимо через р точку перетину прямих l1 і l2.
U1 і U2 розділимі вертикаллю l.
U2. Кожна із цих двох вершин може бути класифікована відносно відрізка [q1,q2] як опукла, опорна або ввігнута. Залежно від класифікації можливі 9 випадків, схематично зображених на малюнку 4.17(а). Усі випадки зрозумілі за винятком випадку (q1,q2) = (ввігнута, ввігнута), який детальніше представлений на малюнку 4.17 (б).
Нехай пряма l1 проходить через
q1 і її правого сусіда на U1.
Аналогічно пряма l2 проходить через
q2 і її лівого сусіда на U2.
Позначимо через р точку перетину прямих l1 і l2.
U1 і U2 розділимі вертикаллю l.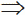 довільна вершина q"
довільна вершина q"  U2прав. відносно q2,
є ввігнутою відносно відрізка [q',q"],
де q'- довільна вершина U1 і U2прав. відносно q2 не розглядається.
Що стосується ланцюга ліворуч від вершини q1,
то для нього не можна це стверджувати.
U2прав. відносно q2,
є ввігнутою відносно відрізка [q',q"],
де q'- довільна вершина U1 і U2прав. відносно q2 не розглядається.
Що стосується ланцюга ліворуч від вершини q1,
то для нього не можна це стверджувати.








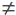 лист) then
лист) then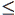 x[v]) then v:= ЛСИН[v] else v:= ПСИН[v];
x[v]) then v:= ЛСИН[v] else v:= ПСИН[v];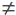 корінь) then
корінь) then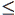 N, то час обробки одного вузла у процедурі СПУСК дорівнює O(logN). А так як глибина дерева Т також рівна O(logN), то час виконання процедури СПУСК дорівнює O(log2N) у гіршому випадку. Процедура ПІДЙОМ дає час O(logN).
N, то час обробки одного вузла у процедурі СПУСК дорівнює O(logN). А так як глибина дерева Т також рівна O(logN), то час виконання процедури СПУСК дорівнює O(log2N) у гіршому випадку. Процедура ПІДЙОМ дає час O(logN).