ГЛАВА 4. ЗАДАЧІ ПОБУДОВИ ОПУКЛОЇ ОБОЛОНКИ
4.1. Постановка задач опуклої оболонки.
Відповідно до визначення, ОО - це найменша опукла множина, яка містить S.
Означення 4.1 Нехай в просторі Ed задано k різних точок p1, p2, ... , pk. Множина точок
p = a1p1 + a2p2 + ... + akpk
(
aj 
R,
aj 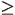
0,
a1 +
a2 + ... +
ak = 1)
Означення 4.2. Опуклою оболонкою conv(L) підмножини L називається найменша опукла множина, яка містить L.
Щоб охарактеризувати структуру conv(L) скінченної множини точок L, необхідно узагальнити поняття опуклого многокутника та опуклого многогранника.
Означення 4.3. Поліедральною множиною в Ed називається перетин скінченної множини замкнутих півпросторів.
Зауваження. Поліедральна множина є опуклою, так як півпростір є опуклою множиною і перетин опуклих множин теж є опуклою множиною. В загальному випадку скінченну d- вимірну поліедральну множину називають опуклим d- політопом ( або просто політопом).
Теорема 4.1 Опукла оболонка скінченної множини точок в Еd є опуклим політопом. Навпаки, кожен опуклий політоп є опуклою оболонкою деякої скінченної множини точок.
Опуклий політоп задається описом його границі, яка складається з граней. Кожна грань опуклого політопа є опуклою множиною; k- грань означає k- вимірну грань. Якщо політоп Р має розмірність d, то його (d - 1) - грані називаються гіпергранями, (d - 2) - грані - підгранями, 1-грані - ребрами, а 0-грані - вершинами.
Число F(d, N) гіперграней d-політопа з N вершинами може набувати таких значень:
Оцінка складності - 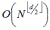 .
.
Позначимо границю опуклої оболонки через CH(S).
Задача ОО1 (ОПУКЛА ОБОЛОНКА). В Еd задано множину S, яка містить N точок. Необхідно побудувати їх опуклу оболонку ( тобто повний опис границі CH(S)).
Задача ОО2 (КРАЙНІ ТОЧКИ). В Еd задано множину S, яка містить N точок. Необхідно визначити ті з них, які є вершинами опуклої оболонки conv(S).
Задача ОО1 асимптотично є такою ж складною, як і задача ОО2, тобто КРАЙНІ ТОЧКИ 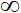 N ОПУКЛА ОБОЛОНКА.
N ОПУКЛА ОБОЛОНКА.
Нижня оцінка задачі пошуку опуклої оболонки: для знаходження опуклої оболонки множини з N точок у просторі d 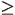 2 необхідно W(NlogN) операцій. Задачу сортування можна за N кроків звести до задачі пошуку опуклої оболонки.
2 необхідно W(NlogN) операцій. Задачу сортування можна за N кроків звести до задачі пошуку опуклої оболонки.
Теорема 4.2 Задача сортування зводиться за лінійний час до задачі побудови опуклої оболонки, і для знаходження впорядкованої опуклої оболонки з N точок на площині потрібен час W(N log N).
Доведення. Нехай задано N додатних дійсних чисел x1, x2, ..., xN. Поставимо у відповідність числу xі точку (xі, xі2) і присвоїмо їй номер і (мал. 4.1).
Мал. 4.1. Ілюстрація доведення теореми 4.2.
Усі ці точки лежать на параболі y=x2. Опукла оболонка цієї множини точок, представлена у стандартному вигляді, буде складатися із списку точок множини, впорядкованого за значенням абсциси. Один перегляд цього списку дозволяє прочитати в потрібному порядку значення xi. Опукла оболонка буде описана послідовністю точок (вершин), х-координати яких будуть упорядковані, тому, маючи опуклу оболонку, можемо отримати впорядкований масив точок х1 х2 ...хN. Нижня оцінка задачі сортування дорівнює нижній оцінці задачі пошуку опуклої оболонки і дорівнює W(N log N).
Означення 4.4. Точка р опуклої множини S називається крайньою, якщо не існує точок а, b  S таких, що р
S таких, що р  (а, b). Звідси випливає, що для того, щоб знайти опуклу оболонку, потрібно виконати наступні два кроки:
(а, b). Звідси випливає, що для того, щоб знайти опуклу оболонку, потрібно виконати наступні два кроки:
- Визначити крайні точки.
- Упорядкувати ці точки так, щоб вони утворили опуклий многокутник.
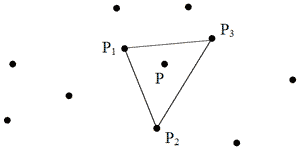
Теорема 4.3. Точка р не є крайньою точкою плоскої опуклої множини S тоді і тільки тоді, коли р лежить у деякому трикутнику р1р2р3, де р1 , р2 , р3  S та р1
S та р1 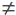 р, р2
р, р2 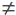 р, р3
р, р3 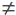 р.$ O(N3) трикутників, які визначаються N точками множини S.
р.$ O(N3) трикутників, які визначаються N точками множини S.
Мал. 4.2. Точка р не є крайньою, бо вона знаходиться всередині трикутника (р1р2р3).
За час O(N3) можна визначити, чи є точка крайньою. Побудова цієї процедури для всіх N точок множини S потребує часу O(N4).
Теорема 4.4. Промінь, який виходить із внутрішньої точки опуклої обмеженої множини S, перетинає її границю в одній точці.
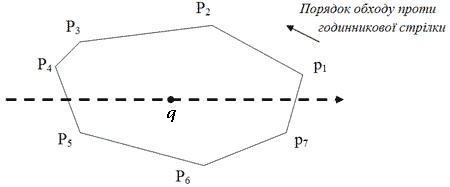
Теорема 4.5. Послідовні вершини опуклого многокутника впорядковані за полярним кутом відносно довільної внутрішньої точки.
Мал. 4.3. Вершини многокутника Р впорядковані відносно точки q.
Якщо відомі крайні точки деякої множини, то опуклу оболонку Р можна знайти, вибравши точку q як внутрішню точку оболонки і впорядкувавши потім крайні точки відповідно до полярного кута відносно q.
Способи знаходження точки q.
- За точку q можна взяти центроїд множини крайніх точок p1, p2, ... , pk: р=(xp, yp),
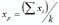 ,
, 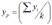 (бо відомо, що центроїд множини точок є внутрішньою точкою опуклої оболонки). Центроїд множини із N точок в k-вимірному просторі може бути тривіально визначений за О(Nk) арифметичних операцій.
(бо відомо, що центроїд множини точок є внутрішньою точкою опуклої оболонки). Центроїд множини із N точок в k-вимірному просторі може бути тривіально визначений за О(Nk) арифметичних операцій.
- Грехем запропонував метод знаходження внутрішньої точки, згідно з яким достатньо взяти центроїд трьох довільних неколінеарних точок, починаючи з двох довільних точок, і по черзі досліджувати N-2 точки, що лишилися, шукаючи серед них одну, яка не лежить на прямій, що визначається першими двома точками. В гіршому випадку для цього потрібен час О(N).
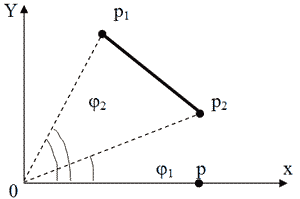
Знайшовши крайні точки множини S, можна за час О(N) знайти точку q, яка є внутрішньою точкою оболонки. Залишається відсортувати (впорядкувати) крайні точки відповідно до значення полярного кута, використовуючи точку q як початок системи координат. Це можна зробити, перетворивши точки до полярної системи координат, за час О(N), а потім відсортувавши їх за час О(NlogN). Нехай на площині задані дві точки р1 і р2. р2 утворює з віссю OX строго менший полярний кут, ніж р1, тоді і лише тоді, коли трикутник (О, р2, р1) має строго додатну площу (мал. 4.4).
Мал. 4.4. Порівняння полярних кутів за допомогою визначення орієнтованої площі D(0, р2 ,р1).
 R, aj
R, aj 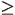 0, a1 + a2 + ... + ak = 1)
0, a1 + a2 + ... + ak = 1) R, aj
R, aj 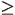 0, a1 + a2 + ... + ak = 1)
0, a1 + a2 + ... + ak = 1)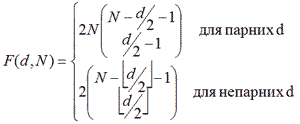
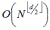 .
.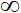 N ОПУКЛА ОБОЛОНКА.
N ОПУКЛА ОБОЛОНКА.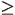 2 необхідно W(NlogN) операцій. Задачу сортування можна за N кроків звести до задачі пошуку опуклої оболонки.
2 необхідно W(NlogN) операцій. Задачу сортування можна за N кроків звести до задачі пошуку опуклої оболонки.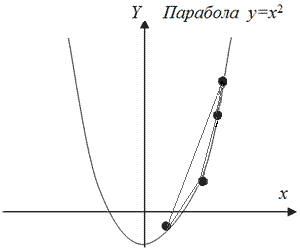
 S таких, що р
S таких, що р  (а, b). Звідси випливає, що для того, щоб знайти опуклу оболонку, потрібно виконати наступні два кроки:
(а, b). Звідси випливає, що для того, щоб знайти опуклу оболонку, потрібно виконати наступні два кроки:
 S та р1
S та р1 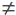 р, р2
р, р2 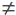 р, р3
р, р3 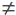 р.$ O(N3) трикутників, які визначаються N точками множини S.
р.$ O(N3) трикутників, які визначаються N точками множини S.
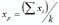 ,
, 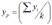 (бо відомо, що центроїд множини точок є внутрішньою точкою опуклої оболонки). Центроїд множини із N точок в k-вимірному просторі може бути тривіально визначений за О(Nk) арифметичних операцій.
(бо відомо, що центроїд множини точок є внутрішньою точкою опуклої оболонки). Центроїд множини із N точок в k-вимірному просторі може бути тривіально визначений за О(Nk) арифметичних операцій.