3.2. ЗАДАЧІ ЛОКАЛІЗАЦІЇ ТОЧКИ
Задачі локалізації точки можна також назвати задачами про приналежність точки. Трудомісткість розв'язання цієї задачі суттєво залежить від природи простору і способу його розбиття. Для сучасного стану обчислювальної геометрії типово те, що плоска задача добре вивчена, але дуже мало відомо про випадок Е3 і ще менше - про випадки більшої розмірності. Розглянемо розбиття площини, або планарні підрозбиття, утворені прямолінійними відрізками. Можна сформулювати такі задачі:
Задача П2. (ПРИНАЛЕЖНІСТЬ ПРОСТОМУ МНОГОКУТНИКУ). Дано простий многокутник Р і точка z; визначити, чи знаходиться точка z всередині Р.
Задача П3. (ПРИНАЛЕЖНІСТЬ ОПУКЛОМУ МНОГОКУТНИКУ). Дано опуклий многокутник Р і точка z; визначити, чи знаходиться точка z всередині Р.
Продемонструємо алгоритм розв'язку для випадку унікального запиту, причому цей результат поширюється і на неопуклі многокутники.
Теорема 3.1 Приналежність точки z внутрішній області простого N-кутника Р можна встановити за час О(n) без передобробки.
Алгоритм
Проведемо через точку горизонталь l (мал. 3.5)
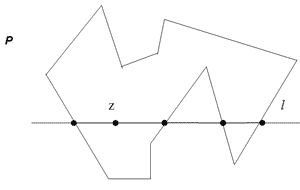
Мал. 3.5.
За теоремою Жордана зовнішня і внутрішня області Р добре визначені.
- Якщо l не перетинає Р, то z зовнішня точка.
- Нехай l перетинає Р.
- випадок, коли l не проходить ні через жодну із вершин Р. Нехай L-число точок перетину l з границею Р ліворуч від z. z лежить всередині тоді і лише тоді, коли L непарне.
- вироджений випадок, коли l проходить через вершини Р.
У роботі [1] пропонується один підхід, хоча не зовсім чіткий і суперечливий такий, що потребує доробки щодо виродженого випадку. Згідно з цим підходом від виродженості позбавляємося, здійснивши нескінчено малий поворот l навколо z проти годинникової стрілки, при цьому:
1) якщо обидві вершини ребра належать l , то це ребро відкидається;
2) якщо рівно одна вершина ребра лежить на l, то перетин враховується, коли ця вершина з великою ординатою, і ігнорується в противному випадку.
Алгоритм виконуються за час О(N). Фрагмент програми матиме вигляд:
begin L:=0;
for i:=1 to N do if ребро (i) не горизонтально
then if (ребро (i) перетинає l нижнім кінцем ліворуч від z)
then L:=L+1;
if ( L непарне) then z всередині else z зовні
end
Для масових запитів розглянемо випадок, коли Р - опуклий многокутник.
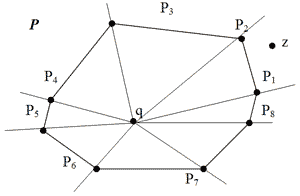
q - довільна внутрішня точка, z - шукана точка. За точку q можна, наприклад, взяти центр мас (центроїд) трикутника, утвореного будь-якою трійкою вершин Р: xq = ( xp1 + xp2 + xp3)/3, yq = ( yp1 + yp2 + yp3)/3
Процедура ПРИНАЛЕЖНІСТЬ ОПУКЛОМУ МНОГОКУТНИКУ
- Дана пробна точка z. Визначаємо методом бінарного пошуку клин, в якому вона лежить. Точка z лежить між променями, які визначаються рi і рi+1
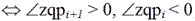 (час О(logN)).
(час О(logN)).
- Якщо рi і рi+1 знайдені, то z - внутрішня точка тоді і лише тоді, коли кут (рiрi+1z) від'ємний ( час О(1)). (q та z по одну сторону від рiрi+1).
Якщо покласти pi=(xi,yi), то визначник, рівний
дає подвоєну орієнтовану площу трикутника (р1р2р3), де "+" 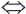 , коли обхід (р1р2р3) орієнтований проти годинникової стрілки(лівий поворот) і "-"
, коли обхід (р1р2р3) орієнтований проти годинникової стрілки(лівий поворот) і "-" 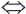 , коли обхід (р1р2р3) орієнтований за годинниковою стрілкою(правий поворот).
, коли обхід (р1р2р3) орієнтований за годинниковою стрілкою(правий поворот).
Мал. 3.6.
Попередня обробка - О(N) для заданої послідовності p1,p2, …, pN.
Терема 3.2. Час відповіді на запит про приналежність точки опуклому N-кутнику рівний О(logN) при витраті O(N) пам'яті і O(N) часу на попередню обробку.
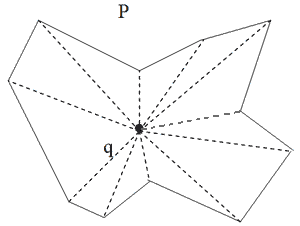
Зірковий многокутник Р містить принаймні одну точку q таку, що [q, pi] лежить повністю всередині многокутника Р для будь-якої вершини pi із P, i=1,…,N, (мал. 3.7). Множина шуканих центрів всередині Р є ядром ЗМ.
Мал. 3.7. Зірковий многокутник.
Терема 3.3. Час відповіді на запит про приналежність точки зірковому N-кутнику рівний О(logN) при витраті O(N) пам'яті і O(N) часу на попередню обробку.


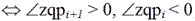 (час О(logN)).
(час О(logN)).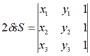
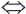 , коли обхід (р1р2р3) орієнтований проти годинникової стрілки(лівий поворот) і "-"
, коли обхід (р1р2р3) орієнтований проти годинникової стрілки(лівий поворот) і "-" 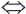 , коли обхід (р1р2р3) орієнтований за годинниковою стрілкою(правий поворот).
, коли обхід (р1р2р3) орієнтований за годинниковою стрілкою(правий поворот).