3.1. Вступ в геометричний пошук.
Означення 3.1 Пошукове повідомлення, відповідно до якого ведеться перегляд файлу, називають пошуковим запитом. Від типу файлу та від набору допустимих запитів залежить його організація та алгоритми обробки запитів.
Означення 3.2 Нехай є набір геометричних даних і необхідно дізнатись, чи мають вони певну властивість (скажімо, опуклість). У найпростішому випадку таке питання виникає один раз. Запит такого типу називається унікальним. Запити, обробка яких повторюється багатократно на тому ж самому файлі, називаються масовими.
Означення 3.3 Передобробкою будемо називати процес розташування даних у зручній для подальшої обробки структурі даних.
Для ефективності пошуку інформацію зручно розташовувати відповідно до деякої структури, при цьому витрачається певний ресурс, і аналіз ефективності алгоритму необхідно зосередити на чотирьох основних мірах його оцінки:
- Час пошуку. Скільки часу треба як в середньому, так і в гіршому випадку для відповіді на одне запитання?
- Пам'ять. Скільки необхідно пам'яті для структури даних?
- Час попередньої обробки. Скільки часу необхідно для організації даних перед пошуком?
- Час коригування. Вказано елемент даних. Скільки треба часу на його включення до структури даних або вилучення з неї?
Як приклад визначення вище названих оцінок розглянемо задачу регіонального пошуку, яка часто виникає в географічних застосуваннях та при управлінні базами даних.
Задача П1 ( РЕГІОНАЛЬНИЙ ПОШУК-ПІДРАХУНОК).
Дано N точок на площині. Скільки із них лежить всередині заданого прямокутника, сторони якого паралельні координатним осям? Тобто, скільки точок (x, y) задовольняють нерівностям a <= x <= b, c <= y <= d для заданих a, b, c і d (мал. 3.1)?
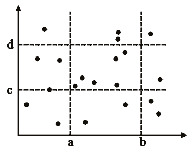
Мал. 3.1. Регіональний запит. Скільки точок всередині прямокутника
Очевидно, що унікальний регіональний запит може бути оброблений (оптимально) за лінійний час, так як необхідно лише перевірити кожну із N точок на задоволення нерівностей, які задають прямокутник. Витрати за пам'яттю теж будуть лінійними, так як слід запам'ятати лише 2N координат. Відсутні витрати на попередню обробку, а час коригування нової точки константний. Для розв'язання задачі, що розглядається, у випадку масових запитів скористаємося методом локусів та методом векторного домінування.
Метод локусів
. Згідно з методом локусів, у геометричних задачах запиту ставиться у відповідність точка в зручному для для пошуку просторі, а цей простір розбивається на області (локуси), у межах яких відповідь не змінюється. Іншими словами, якщо вважати еквівалентними два запити, на які поступають однакові відповіді, то кожна область розбиття простору пошуку відповідає одному класу еквівалентності запитів.
Прямокутник сам по собі - не зручний об'єкт для дослідження, тому розглядатимемо його вершини. Це означає, наприклад, що можна замінити запит з прямокутником чотирма підзадачами, по одній на кожну із його вершин, і сумістити їх розв'язки для одержання остаточної відповіді.
Підзадача, пов'язана з вершиною р, полягає у визначенні кількості точок Q(p) заданої множини, які задовольняють нерівностям x <= x(p) і y <= y(p), тобто кількості точок у лівому нижньому квадранті, визначеному р (мал. 3.2).
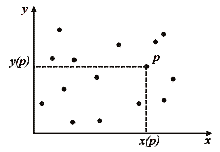
Мал.3.2. Скільки точок "південно - західніше" р?
Метод векторного домінування
Означення 3.4 Векторне домінування. Кажуть, що точка(вектор) v домінує над w, якщо "i виконується vi > wi. На площині точка v домінує над w тоді і лише тоді, коли w лежить у лівому нижньому квадранті, який визначається v. Між домінуванням та регіональним пошуком існує безпосередній зв'язок (мал. 3.3).Нехай Q(p)-число точок, над якими домінує р. Тоді число точок N(p1p2p3p4), які належать прямокутнику p1p2p3p4, визначається таким чином:
N(p1p2p3p4 ) = Q(p1)- Q(p2)- Q(p4)+ Q(p3) (3.1)
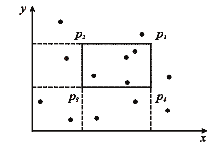
Мал. 3.3. Регіональний пошук у формі чотирьох запитів про домінування.
Це випливає із комбінаторного правила включення-виключення: над усіма точками прямокутника домінує вершина р1. Необхідно виключити такі точки, над якими домінують р2 і р4, але це веде до того, що частина точок буде виключена двічі, а саме ті, над якими домінують і р2, і р4, але якраз ці точки лежать у лівому нижньому квадранті вершини р3.
Таким чином, задача регіонального пошуку зведена до задачі обробки запитів про домінування для чотирьох точок. Властивість, яка спрощує ці запити, полягає у тому, що на площині існують області зручної форми, всередині яких число домінування Q є константою.
Припустимо, що із наших точок на осі x і y опущені перпендикуляри, а отримані лінії продовжені у нескінченність. Вони утворюють решітку із (N+1)2 прямокутників, як показано на мал. 3.4.
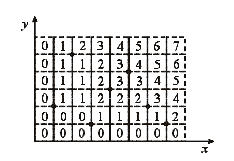
Мал.3.4. Прямокутна решітка для домінантного пошуку.
Для усіх точок р у кожному такому прямокутнику (комірці) Q(p)- константа. Це означає, що домінантний пошук є просто відповідь на питання: у якій комірці прямокутної решітки лежить задана точка?
Після упорядкування початкових точок за обома координатами залишається виконати два двійкових пошуки (по одному для кожної осі), щоб знайти комірку, яка містить шукану точку. Час запиту буде рівним O(logN). Маємо O(N2) комірок, тому необхідна квадратична пам'ять. Визначення числа домінування для будь-якої комірки можна зробити за час O(N), що призводить до загальної витрати часу O(N3) на попередню обробку.
Основні моделі задач геометричного пошуку:
- Задачі локалізації , коли файл являє собою розбиття геометричного простору на області, а запит є точка. Локалізація полягає у визначені області, яка містить шукану точку.
- Задачі регіонального пошуку, коли файл містить набір точок простору, а запит є деяка стандартна геометрична фігура, яка довільно переміщується у цьому просторі (типовий запит у 3-вимірному просторі - це куля або брус). Регіональний пошук полягає у визначені (задача звіту) або у підрахунку кількості (задача підрахунку) всіх точок всередині заданого регіону (області).




