2.3. Реберний список з подвійними зв'язками ( РСПЗ).
Нехай V = {v1, v2, …, vN }, а E = {e1, e2,…,eM }. Головна компонента РСПЗ для планарного графа (V, E) це реберний вузол, який містить чотири інформаційні поля ( V1, V2, F1, F1 ) і два поля вказівників (P1 і P2).
Поле V1 - містить початок ребра, поле V2 - містить його кінець; так ребро отримує умовну орієнтацію. Поля F1 і F1 містять імена граней, які лежать відповідно ліворуч і праворуч від ребра, орієнтованого від V1 до V2.
Вказівник P1 ( відповідно P2 ) задає реберний вузол, який містить перше ребро, яке зустрічається слідом за ребром (V1, V2), при повороті від нього проти годинникової стрілки навколо V1 (відповідно V2). Імена граней і вершин можуть бути задані цілими числами.
Приклад.1 На малюнку 1.3 показано фрагмент РСПЗ.
|
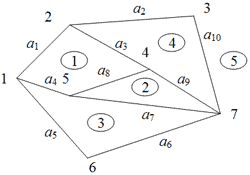
V1 |
V2 |
F1 |
F2 |
P1 |
P2 |
| a1 |
1 |
2 |
5 |
1 |
5 |
3 |
| a2 |
2 |
3 |
5 |
4 |
1 |
10 |
| a3 |
2 |
4 |
4 |
1 |
2 |
8 |
| a4 |
1 |
5 |
1 |
3 |
1 |
7 |
| a5 |
1 |
6 |
3 |
5 |
4 |
6 |
| a6 |
6 |
7 |
3 |
5 |
5 |
10 |
| a7 |
5 |
7 |
2 |
3 |
8 |
6 |
| a8 |
5 |
4 |
1 |
2 |
4 |
9 |
| a9 |
4 |
7 |
4 |
2 |
3 |
7 |
| a10 |
3 |
7 |
5 |
4 |
2 |
9 |
Мал. 1.3 РСПЗ
Можна описати варіант програмної реалізації для заданого прикладу . Якщо граф має N вершин та F граней. Ввівши масиви HV[1:N] та HF[1:F], які містять номери ребер, що виходить з відповідної вершини, опишемо процедуру per, яка заповнює ці масиви за лінійний час.
per
for i
1
to N
do
begin
if (HV[V1[i]] = 0)
then HV[V1[i]]
i;
if (HV[V2[i]] = 0)
then HV[V2[i]]
i;
if (HF[F1[i]] = 0)
then HF[F1[i]]
i;
if (HF[F2[i]] = 0)
then HF[F2[i]]
i;
end;
У результаті виконання процедури per масиви HV та HF для заданого прикладу набудуть таких значень: HV = [1,1,2,3,4,5,6], HF = [1,7,4,2,1].
Можна описати процедуру vertex ( k ), яка будує послідовність ребер, інцидентних vi як послідовність адрес, занесених в масив B.
Vertex ( k )
k
1;
a
HV[k];
ao
a;
B[k]
a;
k
k + 1;
if (V
1[a] = k)
then a
P1[a]
else a
P
2[a];
while (a
ao)
do
begin
B[k]
a; i
i + 1;
if (V
1[a] = k)
then a
P1[a]
else a
P2[a];
end;
Час роботи процедури Vertex ( k ) пропорційний числу ребер, інцидентних vj. Аналогічно можна створити й інші процедури, за дпомогою яких, наприклад, можна було б отримати послідовність ребер, які обмежують грань fj (замінивши в попередній процедурі (HV, V1) на (HF, F1)).